题目内容
已知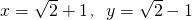
，求x2+3xy+y2的值．
解：∵，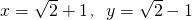
∴（x+y）2=8，xy=1，
∵x2+3xy+y2=x2+2xy+y2+xy，
∴x2+3xy+y2=（x+y）2+xy，
原式=8+1，
=9．
分析：由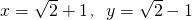可以得出（x+y）2=8，xy=1，再将结论变形就可以求出结论．
点评：本题考查了二次根式的化简求值，考查了完全平方公式的运用，平方差公式的运用．
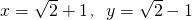，∴（x+y）2=8，xy=1，
∵x2+3xy+y2=x2+2xy+y2+xy，
∴x2+3xy+y2=（x+y）2+xy，
原式=8+1，
=9．
分析：由
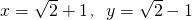可以得出（x+y）2=8，xy=1，再将结论变形就可以求出结论．点评：本题考查了二次根式的化简求值，考查了完全平方公式的运用，平方差公式的运用．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
，求x2+3xy-4y2的值.
，求m-20012的值.
，求x2-3xy+y2的值．
，求x2-3xy+y2的值．