题目内容
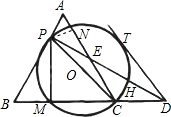
如图,已知:在△ABC中,AB=BC=CA=2,D为BC延长线上一点,CD=1,P为AB上一动点(不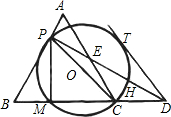 运动至点A,B),以PC为直径作⊙O交BC于M,连接PD,交⊙O于H,交AC于E,连接PM.
运动至点A,B),以PC为直径作⊙O交BC于M,连接PD,交⊙O于H,交AC于E,连接PM.
(1)设AP=t,S△PCD=S,求S关于t的函数解析式和t的取值范围;
(2)过D作⊙O的切线DT,T为切点,试用含t的代数式表示DT的长;
(3)当点P运动到AB中点时,求证: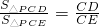 .
.
(1)解:∵PC是直径,
∴PM⊥BC,
在Rt△PBM中,PB=2-t,∠B=60°,
∴PM=PB•sin60°=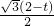 ,
,
S= ×CD×PM=
×CD×PM=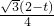 (0<t<2).
(0<t<2).
(2)解:由(1)可知,BM= (2-t),MC=2-BM=
(2-t),MC=2-BM= (2+t),MD=MC+1=2+
(2+t),MD=MC+1=2+ t;
t;
由切割线定理得DT2=DC•DM=2+ t,
t,
∴DT=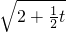 .
.
(3)证明:作PN⊥AC于N;
∵点P为AB中点,
∴CP为等边△ABC的中线,
∴PC平分∠ACB,
∵PM=PN,
∴S△PCD= PM•CD,S△PCE=
PM•CD,S△PCE= PN•CE,
PN•CE,
∴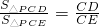 .
.
分析:(1)表示面积关键是确定△PCD的底CD,高PM,围绕求PM,解直角△BPM,其中PB=2-t,∠B=60°;
(2)运用切割线定理得DT2=DC•DM,关键是会表示DM,由(1)可得到启发;
(3)△PCD的底CD,高PM,可以思考△PCE的底CE,构造CE边上的高PN即可.
点评:本题考查了三角形面积的表示方法,等边三角形的性质,角平分线性质,切割线定理,解直角三角形等知识的运用.
∴PM⊥BC,
在Rt△PBM中,PB=2-t,∠B=60°,
∴PM=PB•sin60°=
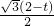 ,
,S=
 ×CD×PM=
×CD×PM=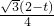 (0<t<2).
(0<t<2).(2)解:由(1)可知,BM=
 (2-t),MC=2-BM=
(2-t),MC=2-BM= (2+t),MD=MC+1=2+
(2+t),MD=MC+1=2+ t;
t;由切割线定理得DT2=DC•DM=2+
 t,
t,∴DT=
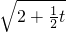 .
.
(3)证明:作PN⊥AC于N;
∵点P为AB中点,
∴CP为等边△ABC的中线,
∴PC平分∠ACB,
∵PM=PN,
∴S△PCD=
 PM•CD,S△PCE=
PM•CD,S△PCE= PN•CE,
PN•CE,∴
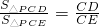 .
.分析:(1)表示面积关键是确定△PCD的底CD,高PM,围绕求PM,解直角△BPM,其中PB=2-t,∠B=60°;
(2)运用切割线定理得DT2=DC•DM,关键是会表示DM,由(1)可得到启发;
(3)△PCD的底CD,高PM,可以思考△PCE的底CE,构造CE边上的高PN即可.
点评:本题考查了三角形面积的表示方法,等边三角形的性质,角平分线性质,切割线定理,解直角三角形等知识的运用.

练习册系列答案
相关题目
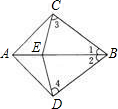
 如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.
如图,已知:在Rt△ABC中,∠C=90°,E为AB的中点,且DE⊥AB于E,若∠CAD:∠DAB=1﹕2,求∠B的度数.

