题目内容
△ABC内接于圆O，AD⊥BC于D交⊙O于E，若BD=8cm，CD=4cm，DE=2cm，则△ABC的面积等于
- A.48cm2
- B.96cm2
- C.108cm2
- D.32cm2
B
分析：根据题意画出图形，要求三角形的面积，底BC=BD+DC可求，只需求出BC边的高，已知DB、DC、DE，利用相交弦定理即可求出高AD，进而求出三角形的面积．
解答：
解：由相交弦定理知：AD•DE=BD•DC，
∵BD=8cm，CD=4cm，DE=2cm，
∴AD=16cm，
又BC=BD+DC=8+4=12cm，
∴S△ABC=
BC•AD=
=96cm2．
故选B．
点评：本题结合三角形的面积考查了相交弦定理，即“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”．熟记并灵活应用定理是解题的关键．
分析：根据题意画出图形，要求三角形的面积，底BC=BD+DC可求，只需求出BC边的高，已知DB、DC、DE，利用相交弦定理即可求出高AD，进而求出三角形的面积．
解答：
解：由相交弦定理知：AD•DE=BD•DC，∵BD=8cm，CD=4cm，DE=2cm，
∴AD=16cm，
又BC=BD+DC=8+4=12cm，
∴S△ABC=
BC•AD==96cm2．故选B．
点评：本题结合三角形的面积考查了相交弦定理，即“圆内两弦相交于圆内一点，各弦被这点所分得的两线段的长的乘积相等”．熟记并灵活应用定理是解题的关键．
练习册系列答案
相关题目
10、如图，正三角形ABC内接于圆O，动点P在圆周的劣弧AB上，且不与A，B重合，则∠BPC等于（ ）
40、如图，△ABC内接于圆O，∠A=50°，∠ABC=60°，BD是圆O的直径，BD交AC于点E，连接DC，则∠AEB等于（ ）
19、如图，正三角形ABC内接于圆O，P是BC所对劣弧上一点，求证：PA=PB+PC．
如图，△ABC为锐角三角形，△ABC内接于圆O，∠BAC=60°，H是△ABC的垂心，BD是⊙O的直径．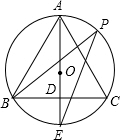
如图，正三角形ABC内接于圆O，AD⊥BC于点D交圆于点E，动点P在优弧BAC上，且不与点B，点C重合，则∠BPE等于