题目内容
如图△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°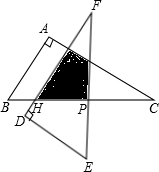 至△DEF的位置,DF交BC于点H.
至△DEF的位置,DF交BC于点H.
(1)PH=______cm.
(2)△ABC与△DEF重叠部分的面积为______cm2.
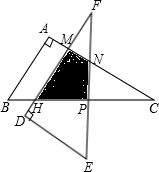 解:设AC与DF和EF的交点分别为M,N,如下图所示:
解:设AC与DF和EF的交点分别为M,N,如下图所示:(1)∵∠A=90°,∠C=30°,BC=12cm,点P为斜面中点,
∴FD=6
 cm,DE=6cm,FP=6cm,
cm,DE=6cm,FP=6cm,根据旋转前后对应角相等可知:△FHP∽△FED,
∴
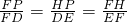 ,即
,即 ,
,解得:PH=2
 ,FH=4
,FH=4 ;
;(2)∵∠C是公共角,∠CPN=∠A=90°,
∴△PNC∽△ABC得,
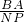 =
=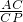 =
=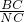 ,即
,即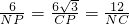 ,其中CP=6,
,其中CP=6,解得NP=2
 ,NC=4
,NC=4 .
.FN=FP-NP=6-2
 ,
,由△FMN∽△CPN,可知
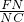 =
=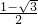 ,
,根据相似三角形面积比等于相似比的平方,可知
S四边形MNPH=S△FHP-S△FMN=S△CNP-(1-
 )S△CNP=6×
)S△CNP=6× ×
× ×
× =9.
=9.△ABC与△DEF重叠部分的面积为9cm2.
故答案为:2
 ,9.
,9.分析:(1)根据旋转前后对应角相等可知:△FHP∽△FED,又点P为斜面中点,FP=6cm,在根据相似三角形的对应边的比相等即可求出PH的长;
(2)把所求阴影部分面积看作△FHP与△FMN的面积差,并且这两个三角形都与△ABC相似,根据∠A=90°,∠C=30°,BC=12cm,求出对应边的长,再根据相似三角形的面积比等于相似比的平方求面积即可.
点评:本题考查了旋转的性质及含30度角的直角三角形的知识,有一定难度,注意相似三角形性质的熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
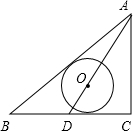 如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )
如图△ABC中,∠C=90°,AC=6,AB=10,D是BC边的中点,以AD上一点O为圆心的圆与AB,BC都相切,则⊙O的半径为( )A、
| ||
B、
| ||
C、
| ||
| D、2 |
 8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为
8、如图△ABC中,AB=3,AC=2,BO平分∠ABC,CO平分∠ACB.DE过点O交AB于D,交AC于E,且DE∥BC.则△ADE周长为 (2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于
(2013•南岗区一模)如图△ABC中,DE∥BC,CD、BE交于点F,若DF=1,CF=3,AD=2,则线段BD的长等于 如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为
如图△ABC中,∠A=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为 如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.
如图△ABC中,∠ABC=20°,外角∠ABF的平分线与CA边的延长线交于点D,外角∠EAC的平分线交BC边的延长线于点H,若∠BDA=∠DAB,则∠AHC=( )度.