题目内容
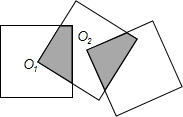 如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是________.
如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是________.
2
分析:根据题意作图,连接O1B,O1C,可得△O1BF≌△O1CG,那么可得阴影部分的面积与正方形面积的关系,同理得出另两个正方形的阴影部分面积与正方形面积的关系,从而得出答案.
解答: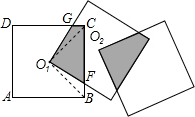 解:连接O1B、O1C,如图:
解:连接O1B、O1C,如图:
∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中
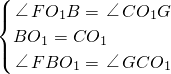
∴△O1BF≌△O1CG,
∴O1、O2两个正方形阴影部分的面积是 S正方形,
S正方形,
同理另外两个正方形阴影部分的面积也是 S正方形,
S正方形,
∴S阴影部分= S正方形=2.
S正方形=2.
故答案为:2.
点评:本题主要考查了正方形的性质及全等三角形的证明,把阴影部分进行合理转移是解决本题的难点,难度适中.
分析:根据题意作图,连接O1B,O1C,可得△O1BF≌△O1CG,那么可得阴影部分的面积与正方形面积的关系,同理得出另两个正方形的阴影部分面积与正方形面积的关系,从而得出答案.
解答:
 解:连接O1B、O1C,如图:
解:连接O1B、O1C,如图:∵∠BO1F+∠FO1C=90°,∠FO1C+∠CO1G=90°,
∴∠BO1F=∠CO1G,
∵四边形ABCD是正方形,
∴∠O1BF=∠O1CG=45°,
在△O1BF和△O1CG中
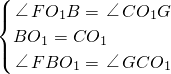
∴△O1BF≌△O1CG,
∴O1、O2两个正方形阴影部分的面积是
 S正方形,
S正方形,同理另外两个正方形阴影部分的面积也是
 S正方形,
S正方形,∴S阴影部分=
 S正方形=2.
S正方形=2.故答案为:2.
点评:本题主要考查了正方形的性质及全等三角形的证明,把阴影部分进行合理转移是解决本题的难点,难度适中.

练习册系列答案
相关题目
 如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是
如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是 (2013•泸州模拟)如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是( )
(2013•泸州模拟)如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是( ) 如图,三个边长均为2cm的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是( )
如图,三个边长均为2cm的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是( )
