Question

如图，在三角形纸片ABC中，∠A=90°、AB=12、AC=5．折叠三角形纸片，使点A在BC边上的点E处，则AD=__________．

Answer 1

．

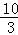【考点】翻折变换（折叠问题）．

【分析】先利用勾股定理求得BC=13，然后由翻折的性质可知BE=8，AD=DE，设AD=DE=x，则BD=12﹣x，最后再Rt△DEB中利用勾股定理求解即可．

【解答】解；在Rt△ABC中，BC===13．

由翻折的性质可知：CE=AD=5，AD=DE，∠CED=∠A=90°．

∵BE=BC﹣CE，

∴BE=13﹣5=8．

设AD=DE=x，则BD=12﹣x．

在Rt△DEB中，由勾股定理得：DB²=DE²+EB²，即（12﹣x）²=x²+8²．

解得：x=．

∴AD=．

故答案为：．

【点评】本题主要考查的是翻折的性质、勾股定理的应用，在Rt△DEB中依据勾股定理列出关于x的方程是解题的关键．