题目内容
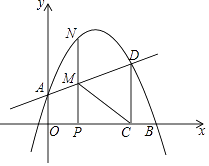
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3, ![]() ),过点D作DC⊥x轴,垂足为C.
),过点D作DC⊥x轴,垂足为C.
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;
(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
【答案】
(1)
解:把点B(4,0),点D(3, ![]() ),代入y=ax2+bx+1中得,
),代入y=ax2+bx+1中得, 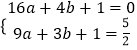 ,
,
解得: 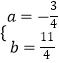 ,
,
∴抛物线的表达式为y=﹣ ![]() x2+
x2+ ![]() x+1
x+1
(2)
解:设直线AD的解析式为y=kx+b,
∵A(0,1),D(3, ![]() ),
),
∴ 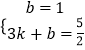 ,
,
∴ ![]() ,
,
∴直线AD的解析式为y= ![]() x+1,
x+1,
设P(t,0),
∴M(t, ![]() t+1),
t+1),
∴PM= ![]() t+1,
t+1,
∵CD⊥x轴,
∴PC=3﹣t,
∴S△PCM= ![]() PCPM=
PCPM= ![]() (3﹣t)(
(3﹣t)( ![]() t+1),
t+1),
∴S△PCM=﹣ ![]() t2+
t2+ ![]() t+
t+ ![]() =﹣
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]() ,
,
∴△PCM面积的最大值是 ![]()
(3)
解:∵OP=t,
∴点M,N的横坐标为t,
设M(t, ![]() t+1),N(t,﹣
t+1),N(t,﹣ ![]() t2+
t2+ ![]() t+1),
t+1),
∴MN=﹣ ![]() t2+
t2+ ![]() t+1﹣
t+1﹣ ![]() t﹣1=﹣
t﹣1=﹣ ![]() t2+
t2+ ![]() t,CD=
t,CD= ![]() ,
,
如果以点M、C、D、N为顶点的四边形是平行四边形,
∴MN=CD,即﹣ ![]() t2+
t2+ ![]() t=
t= ![]() ,
,
∵△=﹣39,
∴方程﹣ ![]() t2+
t2+ ![]() t=
t= ![]() 无实数根,
无实数根,
∴不存在t,使以点M、C、D、N为顶点的四边形是平行四边形.
【解析】(1)把B(4,0),点D(3, ![]() )代入y=ax2+bx+1即可得出抛物线的解析式;(2)先用含t的代数式表示P、M坐标,再根据三角形的面积公式求出△PCM的面积与t的函数关系式,然后运用配方法可求出△PCM面积的最大值;(3)若四边形BCMN为平行四边形,则有MN=DC,故可得出关于t的二元一次方程,解方程即可得到结论.
)代入y=ax2+bx+1即可得出抛物线的解析式;(2)先用含t的代数式表示P、M坐标,再根据三角形的面积公式求出△PCM的面积与t的函数关系式,然后运用配方法可求出△PCM面积的最大值;(3)若四边形BCMN为平行四边形,则有MN=DC,故可得出关于t的二元一次方程,解方程即可得到结论.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 阅读快车系列答案
阅读快车系列答案【题目】汶川地震牵动着全国亿万人民的心,某校为地震灾区开展了“献出我们的爱” 赈灾捐款活动.八年级(1)班50名同学积极参加了这次赈灾捐款活动,下表是小明对全班捐款情况的统计表:
捐款(元) | 10 | 15 | 30 |
| 50 | 60 |
人数 | 3 | 6 | 11 |
| 13 | 6 |
因不慎两处被墨水污染,已无法看清,但已知全班平均每人捐款38元.
(1)根据以上信息请帮助小明计算出被污染处的数据,并写出解答过程.
(2)该班捐款金额的众数、中位数分别是多少?