题目内容
只有两个正整数介于分数 与
与 之间,则正整数n的所以可能值之和是多少?
之间,则正整数n的所以可能值之和是多少?
解:∵ <
< .
.
∵4< <5,
<5,
又已知只有两个正整数介于分数 与
与 之间,
之间,
∴介于分数 与
与 之间的两个正整数是3和4,
之间的两个正整数是3和4,
∴分数 应满足2<
应满足2< <3,
<3,
解不等式组2< <3,
<3,
得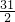 <n<50,
<n<50,
因此,满足条件的正整数n为16、17、18、19…49,
它们的和为: =1105.
=1105.
分析:根据分数的基本性质,一个分子、分母都是正数的分数,其分子、分母同时加上一个相同的正数,其分数的值会变小,列出不等式,再根据只有两个正整数介于分数 与
与 之间,进一步判断正整数n的值的大小.
之间,进一步判断正整数n的值的大小.
点评:此题较难,要根据分式的性质对原式进行适当放缩,得到合适的取值范围,再进行筛选,得到所需整数值.
 <
< .
.∵4<
 <5,
<5,又已知只有两个正整数介于分数
 与
与 之间,
之间,∴介于分数
 与
与 之间的两个正整数是3和4,
之间的两个正整数是3和4,∴分数
 应满足2<
应满足2< <3,
<3,解不等式组2<
 <3,
<3,得
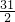 <n<50,
<n<50,因此,满足条件的正整数n为16、17、18、19…49,
它们的和为:
 =1105.
=1105.分析:根据分数的基本性质,一个分子、分母都是正数的分数,其分子、分母同时加上一个相同的正数,其分数的值会变小,列出不等式,再根据只有两个正整数介于分数
 与
与 之间,进一步判断正整数n的值的大小.
之间,进一步判断正整数n的值的大小.点评:此题较难,要根据分式的性质对原式进行适当放缩,得到合适的取值范围,再进行筛选,得到所需整数值.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目