Question

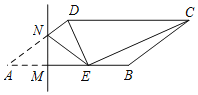
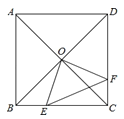
【题目】如图，在梯形中，，，.点为边的中点，以为顶点作，射线交腰于点，射线交腰于点，联结.

（1）求证：；

（2）若是以为腰的等腰三角形，求的长；

（3）若，求的长.

Answer 1

【答案】（1）见解析；（2）或；（3）.

【解析】

（1）先根据相似三角形的判定证出：，从而得出，再结合已知条件可得：，从而证出：.

（2）根据腰的情况分类讨论：①若BM=EM=3时，根据相似三角形的性质，可证出：FM=EF，CF=FM，从而证出：∠B＝∠FMB，再根据平行线的判定即可得：MF∥AB，连接DM根据平行四边形的判定可得：四边形ABMD是平行四边形，从而证出：MD∥AB，故可判定此时D、F重合，从此得出EF=FM=FC=DC=6；②若BM=BE=3时，易证EF为梯形ABCD的中位线，从而求出EF；

（3）根据相似三角形的性质和已知条件可得：，过点作，过点A作，然后求出cosB，设，则，根据勾股定理：，根据BH＋HM=BM即可求出BE.

（1）在梯形中，

，，

，

，

又，

.

.

.

，

，即.

又，

.

（2）∵，点为边的中点

∴BM=

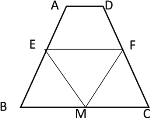
①若BM=EM=3时

∵，

∴，

∴FM=EF

∵

∴

∴CF=FM

∴∠C＝∠FMB

∴∠B＝∠FMB

∴MF∥AB

连接DM

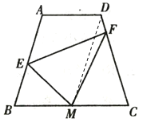
∵AD=BM=3，AD∥BM

∴四边形ABMD是平行四边形

∴MD∥AB

∴此时D、F重合

∴EF=FM=FC=DC=6；

②若BM=BE=3时，

∴E为AB的中点

∵

∴

∴CF=CM=3

∴F为CD的中点

∴EF为梯形ABCD的中位线

∴EF=

综上所述：或.

（3），，，

.

过点作，过点A作

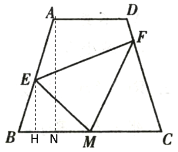
∴BN=

∴cosB=

设，

则，根据勾股定理：，

∵BH＋HM=BM

∴，

.