题目内容
【题目】已知![]() .
.

(1)如图1,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() .试说明:
.试说明:![]() ;
;
(2)如图2,若![]() ,
,![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 、
、![]() ,那么
,那么![]() (只要直接填上正确结论即可).
(只要直接填上正确结论即可).
【答案】(1)见解析;(2) 49°.
【解析】
(1)首先作FG∥AB,根据直线AB∥CD,可得EF∥CD,据此推得∠ABF+∠CDF=∠BFD即可,再根据BF,DF分别平分∠ABE,∠CDE,推得∠ABF+∠CDF=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,据此推得∠BFD=![]() ∠BED;
∠BED;
(2) 连接BD,先求出∠MBD+∠NDB的度数,再求出∠PBM+∠PDN的度数,再利用三角形内角和定理即可解决;
(3)连接BD,先求出∠MBD+∠NDB的度数,再求出∠PBM+∠PDN的度数,再利用三角形内角和定理即可解决.
(1)如图1,作FG∥AB,
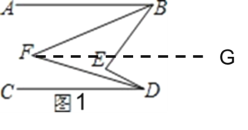
∵直线AB∥CD,
∴FG∥CD,
∴∠ABF=∠BFG,∠CDF=∠GFD,
∴∠ABF+∠CDF=∠BFG+∠GFD=∠BFD,
即∠ABF+∠CDF=∠BFD,
∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∴∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(2)连接BD,
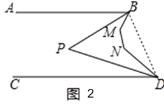
∵∠BMN=133°,∠MND=145°,
∴∠MBD+∠NDB=360°-(133°+145°)=82°,
∵BP、DP分别平分∠ABM、∠NDC,
∴∠PBM=![]() ∠ABM,∠PDN=
∠ABM,∠PDN=![]() ∠CDN,
∠CDN,
∴∠PBM+∠PDN=![]() (180°-82°)=49°,
(180°-82°)=49°,
∴∠BPD=180°-(∠MBD+∠NDB)-(∠PBM+∠PDN)=49°.
故答案为49°.

 科学实验活动册系列答案
科学实验活动册系列答案