Question

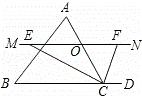
如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC，设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F．

（1）探究：线段OE与OF的数量关系并加以证明；

（2）当点O运动到何处，且△ABC满足什么条件时，四边形AECF是正方形？

（3）当点O在边AC上运动时，四边形BCFE会是菱形吗？若是，请证明，若不是，则说明理由．

Answer 1

（1）解：OE=OF．理由如下：

∵CE是∠ACB的角平分线，

∴∠ACE=∠BCE，

又∵MN∥BC，

∴∠NEC=∠ECB，

∴∠NEC=∠ACE，

∴OE=OC，

∵CF是∠BCA的外角平分线，

∴∠OCF=∠FCD，

又∵MN∥BC，

∴∠OFC=∠ECD，

∴∠OFC=∠COF，

∴OF=OC，

∴OE=OF；

（2）△ABC满足∠ACB为直角的直角三角形时，四边形AECF是正方形．

∵当点O运动到AC的中点时，AO=CO，

又∵EO=FO，

∴四边形AECF是平行四边形，

∵FO=CO，

∴AO=CO=EO=FO，

∴AO+CO=EO+FO，即AC=EF，

∴四边形AECF是矩形．

已知MN∥BC，当∠ACB=90°，则

∠AOF=∠COE=∠COF=∠AOE=90°，

∴AC⊥EF，

∴四边形AECF是正方形．

（3）解：不可能．

如图所示，

∵CE平分∠ACB，CF平分∠ACD，

∴∠ECF=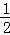∠ACB+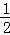∠ACD=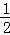（∠ACB+∠ACD）=90°，

若四边形BCFE是菱形，则BF⊥EC，

但在△GFC中，不可能存在两个角为90°，所以不存在其为菱形．