题目内容
12.如图,依次连接一个面积为4的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第六个正方形的面积是($\frac{1}{2}$)5,第2017个正方形的面积是($\frac{1}{2}$)2016.
分析 根据正方形的性质及三角形中位线的定理可分别求得第二个,第三个正方形的面积从而不难发现规律,根据规律即可求得第2017个正方形的面积.
解答 解:根据三角形中位线定理得,
第二个正方形的边长为$\sqrt{(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}$=$\sqrt{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,面积为:$\frac{1}{2}$,
第三个正方形的面积为$\frac{1}{4}$=($\frac{1}{2}$)2,
以此类推,
第六个正方形的面积为:($\frac{1}{2}$)5,
第2017个正方形的面积为:($\frac{1}{2}$)2016.
故答案为:($\frac{1}{2}$)5,($\frac{1}{2}$)2016.
点评 此题主要考查了中点四边形,根据中位线定理和正方形的性质计算出正方形的面积,找出规律,即可解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列事件是不确定事件的是( )
| A. | 守株待兔 | B. | 水中捞月 | C. | 风吹草动 | D. | 水涨船高 |
3.下列数中,是无理数的是( )
| A. | 0 | B. | -$\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | 2 |
20.在△ABC中,∠C=90°,AC=4,AB=5,以点C为圆心,以R长我半径画圆,若⊙C与边AB只有一个公共点,则R的取值范围是( )
| A. | R=$\frac{12}{5}$ | B. | 3≤R≤4 | C. | 0<R<3或R>4 | D. | 3<R≤4或R=$\frac{12}{5}$ |
7.下列命题中,不正确的是( )
| A. | 有一组邻边相等的平行四边形是菱形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 对角线垂直的平行四边形是正方形 | |
| D. | 一组对边平行且相等的四边形是平行四边形 |
17.计算:(-2)-5=( )
| A. | 3 | B. | -3 | C. | -7 | D. | 7 |
11.在2,-$\frac{5}{2}$,0,-2.3中最小的有理数是( )
| A. | $-\frac{5}{2}$ | B. | -2.3 | C. | 2 | D. | 0 |
12.下面各对数中,结果相等的是( )
| A. | -32和(-3)2 | B. | -(-3)2和-(2)3 | C. | -(-3)2和-32 | D. | -2×32和-3×22 |
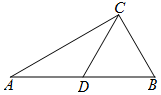 如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E,
如图,在△ABC中,∠ACB=90°,点D是AB的中点,过点D作DE⊥AC于点E,