题目内容
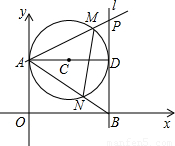 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则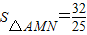 时,k= .
时,k= .
【答案】分析:首先连接DN.由直径所对的圆周角是直角,可得∠AND=90°,易证得△AMN∽△ABP;又由OA与PB都是⊙C的切线,易证得四边形OADB是矩形,把x=0代入y=kx+3得y=3,即OA=BD=3,然后由勾股定理求得AB=5;又由相似三角形的相似比推知相似三角形的面积比.然后分两种情况进行讨论:①当点P在B点上方时,由相似三角形的面积比得到k2-4k-2=0,解关于k的一元二次方程;②当点P在B点下方时,由相似三角形的面积比得到k2+1=-(4k+3),解关于k的一元二次方程.
解答:解:连接DN.
∵AD是⊙C的直径,
∴∠AND=90°,
∵∠ADN=90°-∠DAN,∠ABD=90°-∠DAN,
∴∠ADN=∠ABD,
又∵∠ADN=∠AMN,
∴∠ABD=∠AMN,
∵∠MAN=∠BAP,
∴△AMN∽△ABP,
∵OA与PB都是⊙C的切线,
∴AD⊥OA,AD⊥PB,
∵∠AOB=90°,
∴四边形OADB是矩形,
∴OB=AD=4,OA=BD,
 把x=0代入y=kx+3得:y=3,即OA=BD=3,
把x=0代入y=kx+3得:y=3,即OA=BD=3,
∴在Rt△OAB中,AB= =5,
=5,
∵S△ABD= AB•DN=
AB•DN= AD•BD,
AD•BD,
∴DN= =
= ,
,
∴AN2=AD2-DN2=42-( )2=
)2= ,
,
∴ ,
,
∴S△AMN=( )2•S△ABP=
)2•S△ABP= ,
,
∵点P的横坐标为4,且直线PA的解析式为:y=kx+3,
∴点P的纵坐标为:4k+3,
当点P在B点上方时,
∵AP2=AD2+PD2=AD2+(PB-BD)2=42+(4k+3-3)2=16(k2+1),
或AP2=AD2+PD2=AD2+(BD-PB)2=42+(3-4k-3)2=16(k2+1),
∴S△ABP= PB•AD=
PB•AD= (4k+3)×4=2(4k+3),
(4k+3)×4=2(4k+3),
∴S△AMN= =
= =
= =
= ,
,
整理得:k2-4k-2=0,
解得:k1=2+ ,k2=2-
,k2=2- ;
;
当点P在B点下方时,
∵AP2=AD2+PD2=42+(3-4k-3)2=16(k2+1),S△ABP= PB•AD=
PB•AD= [-(4k+3)]×4=-2(4k+3),
[-(4k+3)]×4=-2(4k+3),
S△AMN= =
= =
= ,
,
化简得:k2+1=-(4k+3),
解得:k=-2,
综上可得:当 时,k=2±
时,k=2± 或k=-2.
或k=-2.
故答案为:2± 或-2.
或-2.
点评:此题考查了切线的性质、相似三角形的判定与性质、矩形的判定与性质以及直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想、分类讨论思想与方程思想的应用.
解答:解:连接DN.
∵AD是⊙C的直径,
∴∠AND=90°,
∵∠ADN=90°-∠DAN,∠ABD=90°-∠DAN,
∴∠ADN=∠ABD,
又∵∠ADN=∠AMN,
∴∠ABD=∠AMN,
∵∠MAN=∠BAP,
∴△AMN∽△ABP,
∵OA与PB都是⊙C的切线,
∴AD⊥OA,AD⊥PB,
∵∠AOB=90°,
∴四边形OADB是矩形,
∴OB=AD=4,OA=BD,
 把x=0代入y=kx+3得:y=3,即OA=BD=3,
把x=0代入y=kx+3得:y=3,即OA=BD=3,∴在Rt△OAB中,AB=
 =5,
=5,∵S△ABD=
 AB•DN=
AB•DN= AD•BD,
AD•BD,∴DN=
 =
= ,
,∴AN2=AD2-DN2=42-(
 )2=
)2= ,
,∴
 ,
,∴S△AMN=(
 )2•S△ABP=
)2•S△ABP= ,
,∵点P的横坐标为4,且直线PA的解析式为:y=kx+3,
∴点P的纵坐标为:4k+3,
当点P在B点上方时,
∵AP2=AD2+PD2=AD2+(PB-BD)2=42+(4k+3-3)2=16(k2+1),
或AP2=AD2+PD2=AD2+(BD-PB)2=42+(3-4k-3)2=16(k2+1),
∴S△ABP=
 PB•AD=
PB•AD= (4k+3)×4=2(4k+3),
(4k+3)×4=2(4k+3),∴S△AMN=
 =
= =
= =
= ,
,整理得:k2-4k-2=0,
解得:k1=2+
 ,k2=2-
,k2=2- ;
;当点P在B点下方时,
∵AP2=AD2+PD2=42+(3-4k-3)2=16(k2+1),S△ABP=
 PB•AD=
PB•AD= [-(4k+3)]×4=-2(4k+3),
[-(4k+3)]×4=-2(4k+3),S△AMN=
 =
= =
= ,
,化简得:k2+1=-(4k+3),
解得:k=-2,
综上可得:当
 时,k=2±
时,k=2± 或k=-2.
或k=-2.故答案为:2±
 或-2.
或-2.点评:此题考查了切线的性质、相似三角形的判定与性质、矩形的判定与性质以及直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
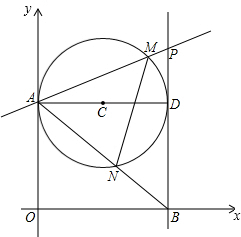 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.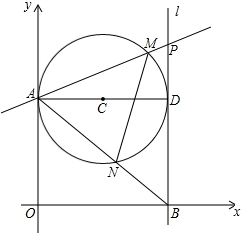 如图,第一象限内半径为4的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+6.
如图,第一象限内半径为4的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+6.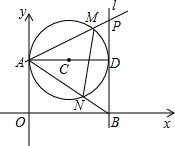 如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则
如图,第一象限内半径为2的⊙C与y轴相切于点A,作直径AD,过点D作⊙C的切线l交x轴于点B,P为直线l上一动点,已知直线PA的解析式为:y=kx+3.设⊙C与PA交于点M,与AB交于点N,则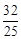 的k值?若存在,请求出符合的k值;若不存在,请说明理由。
的k值?若存在,请求出符合的k值;若不存在,请说明理由。