题目内容
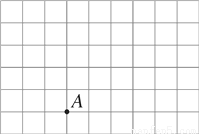
在如图所示的网格中,每个小正方形的边长都为1.
(1)试作出直角坐标系,使点A的坐标为(2,-1);
(2)在(1)中建立的直角坐标系中描出点B(3,4),C(0,1),并求三角形ABC的面积.
练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
题目内容
在如图所示的网格中,每个小正方形的边长都为1.
(1)试作出直角坐标系,使点A的坐标为(2,-1);
(2)在(1)中建立的直角坐标系中描出点B(3,4),C(0,1),并求三角形ABC的面积.

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案