题目内容
(1)用计算器探索:
①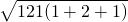 =
=
②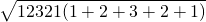 =
=
③ =
=
由此猜想: =______.
=______.
(2)已知关于x的方程x2-2ax+a2-2a+2=0的两个实数根x1、x2满足x12+x22=2,则a的值为______.
解:(1)由①可得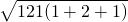 =22;
=22;
②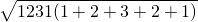 =333;
=333;
③ =4444;
=4444;
故猜想: =7777777.
=7777777.
(2)∵x1、x2是关于x的方程x2-2ax+a2-2a+2=0的两个实数根,∴x1+x2=2a,x1x2=a2-2a+2,
又∵x12+x22=2,即(x1+x2)2-2x1x2=2,即4a2-2(a2-2a+2)=2,整理得(2a-2)(a+3)=0,即a=1或a=-3.
把a=1代入原方程得x2-2x+12-2+2=0,△=(-2)2-4(12-2+2)=0,方程有两个相等的实数根;
把a=-3代入原方程得x2-2×(-3)x+(-3)2-2(-3)+2=0,即x2+6x+17=0,△=(6)2-4×17=-32<0,与已知相矛盾,故a的值为1.
分析:(1)根据①②③找出规律;求出 的值;
的值;
(2)根据一元二次方程根与系数的关系,以及x12+x22=2即(x1+x2)2-2x1x2=2,求出a的值;
点评:(1)属于规律性题目,主要是根据已知中所给的式子找出规律,求解;
(2)根据一元二次方程根与系数的关系,求出a的值,解答此类题目时要注意验根,否则会造成误解.
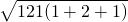 =22;
=22;②
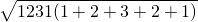 =333;
=333;③
 =4444;
=4444;故猜想:
 =7777777.
=7777777.(2)∵x1、x2是关于x的方程x2-2ax+a2-2a+2=0的两个实数根,∴x1+x2=2a,x1x2=a2-2a+2,
又∵x12+x22=2,即(x1+x2)2-2x1x2=2,即4a2-2(a2-2a+2)=2,整理得(2a-2)(a+3)=0,即a=1或a=-3.
把a=1代入原方程得x2-2x+12-2+2=0,△=(-2)2-4(12-2+2)=0,方程有两个相等的实数根;
把a=-3代入原方程得x2-2×(-3)x+(-3)2-2(-3)+2=0,即x2+6x+17=0,△=(6)2-4×17=-32<0,与已知相矛盾,故a的值为1.
分析:(1)根据①②③找出规律;求出
 的值;
的值;(2)根据一元二次方程根与系数的关系,以及x12+x22=2即(x1+x2)2-2x1x2=2,求出a的值;
点评:(1)属于规律性题目,主要是根据已知中所给的式子找出规律,求解;
(2)根据一元二次方程根与系数的关系,求出a的值,解答此类题目时要注意验根,否则会造成误解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
用计算器探索:已知按一定规则排列的一组数:1,
,
,…,
,
,如果从中选出若干个数,使它们的和大于3,那么至少要选几个数( )
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| A、3个数 | B、4个数 |
| C、5个数 | D、6个数 |