题目内容
如图,在锐角△ABC中,AD、CE分别是BC、AB边上的高,AD、CE相交于F, BF的中点为P,AC的中点为Q,连接PQ、DE.
(1)求证:直线PQ是线段DE的垂直平分线;
(2)如果△ABC是钝角三角形,∠BAC>90°,那么上述结论是否成立? 请按钝角三角形改写原题,画出相应的图形,并给予必要的说明.

证明(1)连接PD、PE、QD、QE.
因为 CE⊥AB,P是BF的中点,
所以 △BEF是直角三角形,且
PE是Rt△BEF斜边的中线,
所以 PE=![]() BF.
BF.
又因为 AD⊥BC,
所以 △![]() BDF是直角三角形,且PD是Rt△BDF斜边的中线,
BDF是直角三角形,且PD是Rt△BDF斜边的中线,
 所以 PD=
所以 PD=![]() BF=PE,
BF=PE,
所以 点P在线段DE的垂直平分线上.
同理可证,QD、QE分别是Rt△ADC和Rt△AEC斜边上的中线,
所以 QD=![]() AC=QE,
AC=QE,
所以 点Q也在线段DE的垂直平分线上.
所以 直线PQ垂直平分线段DE.
(2)当△ABC为钝角三角形时,(1)中的结论仍成立.
如右图,△ABC是钝角三角形,∠BAC>90°.
原题改写为:如右图,在钝角△ABC中,AD、CE分别是BC、AB边上的高,DA 与CE的延长线交于点F,BF的中点为P,AC的中点为Q,连接PQ、DE.
求证:直线PQ垂直且平分线段DE.
证明 连接PD,PE,QD,QE,则PD、PE分别是Rt△BDF和Rt△BEF的中线,
所以 PD=![]() BF, PE=
BF, PE=![]() BF,
BF,
所以 PD=PE,
点P在线段DE的垂直平分线上.
同理可证 QD=QE,
所以 点Q在线段DE的垂直平分线上.
所以 直线PQ垂直平分线段DE.

 如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
如图,在锐角△ABC中,以BC为直径的半圆O分别交AB,AC与D、E两点,且cosA=
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
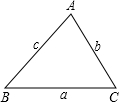 如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答:
如图,在锐角△ABC中,a>b>c,以某任意两个顶点为顶点作矩形,第三个顶点落在以这两个顶点所确定的对边上,这样可以作三个面积相等的矩形,请问这三个矩形的周长大小关系如何?(记ta、tb、tc分别以a、b、c为边的矩形的周长)答: 25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.
25、如图,在锐角△ABC中,AB>AC,AD⊥BC于D,以AD为直径的⊙O分别交AB,AC于E,F,连接DE,DF.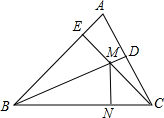 如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=
如图,在锐角△ABC中,∠ABC的平分线交AC于点D,AB边上的高CE交BD于点M,过点M作BC的垂线段MN,若EC=4,∠BCE=45°,则MN=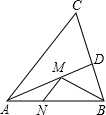 如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是
如图,在锐角△ABC中,AB=4,∠BAC=45°.∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点.则BM+MN的最小值是