题目内容
 已知:如图,梯形ABCD中,AD∥BC,AB=a,AD=b,∠A=2∠C,则BC长为
已知:如图,梯形ABCD中,AD∥BC,AB=a,AD=b,∠A=2∠C,则BC长为
- A.

- B.

- C.a+b
- D.a+2b
C
分析:此题的关键是作辅助线,将已知条件中线段长转化到BC上,从而求出BC.
解答: 解:作AE∥CD交BC于E,
解:作AE∥CD交BC于E,
∴平行四边形ADCE,
∴∠C=∠DAE,
又∠AEB=∠C,∠A=2∠C,
∴∠BAE=∠BEA,
∴BE=AB=a,
又CE=AD=b,
∴BC=BE+CE=a+b.
故选C.
点评:此题中主要是通过平移一腰,得到一个平行四边形和一个等腰三角形.根据平行四边形的性质和等腰三角形的性质进行计算.
分析:此题的关键是作辅助线,将已知条件中线段长转化到BC上,从而求出BC.
解答:
 解:作AE∥CD交BC于E,
解:作AE∥CD交BC于E,∴平行四边形ADCE,
∴∠C=∠DAE,
又∠AEB=∠C,∠A=2∠C,
∴∠BAE=∠BEA,
∴BE=AB=a,
又CE=AD=b,
∴BC=BE+CE=a+b.
故选C.
点评:此题中主要是通过平移一腰,得到一个平行四边形和一个等腰三角形.根据平行四边形的性质和等腰三角形的性质进行计算.

练习册系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )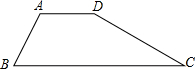 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=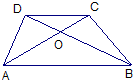 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.