题目内容
如图,在梯形ABCD中,AB‖CD,∠A=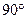 ,AB=3,CD=6,BE⊥BC交直线AD于点E.
,AB=3,CD=6,BE⊥BC交直线AD于点E.

(1)当点E与D恰好重合时,求AD的长;
(2)当点E在边AD上时(E不与A、D重合),设AD=x,ED=y,试求y关于x的函数关系式,并写出定义域;
(3)问:是否可能使△ABE、△CDE与△BCE都相似?若能,请求出此时AD的长;若不能,请说明理由.
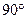 ,AB=3,CD=6,BE⊥BC交直线AD于点E.
,AB=3,CD=6,BE⊥BC交直线AD于点E. 
(1)当点E与D恰好重合时,求AD的长;
(2)当点E在边AD上时(E不与A、D重合),设AD=x,ED=y,试求y关于x的函数关系式,并写出定义域;
(3)问:是否可能使△ABE、△CDE与△BCE都相似?若能,请求出此时AD的长;若不能,请说明理由.
(1)3
(2)
 ,
,
(3)

解:(1)当点E与D重合时,由∠ABD=∠BDC,∠DBC=∠A,
得△ABD∽△BDC,则 ,---------------------(2分)
,---------------------(2分)
∴ ,-----------------------------------------(1分)
,-----------------------------------------(1分)
则 .------------------------------(1分)
.------------------------------(1分)
(2)作BH⊥DC,H为垂足,
则∠ABE+∠EBH=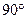 , ∠EBH+∠HBC=
, ∠EBH+∠HBC=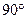 ,
,
∴∠HBC=∠ABE,又∠BHC=∠A=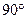 ,
,
∴△ABE∽△HBC,------------------------------------(2分)
又AB‖CD,得HB=AD=x,HC= ,
,
∴ ,即
,即 ,--------------------------(2分)
,--------------------------(2分)
解得 ,定义域为
,定义域为 .----------------------(1分)
.----------------------(1分)
(3)假设能使△ABE、△CDE与△BCE都相似,当点E在边AD上时,(如图1)

易知∠EBC=∠A=∠D=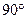 ,
,
考虑∠1的对应角,容易得到∠1 ,∠1
,∠1 ,
,
所以必有∠1=∠2=∠3= ,
,
于是在△ABE、△CDE中,易得 ,
, ,
,
∴ ,------------------------------------------(2分)
,------------------------------------------(2分)
此时, ,
, , BC="6," ----------------
, BC="6," ---------------- -(1分)
-(1分)
即能使△ABE、△CDE与△BCE都相似;当点E在边AD的延长线上时,(如图2)

类似分析可得∠1=∠2=∠3= ,可求得
,可求得 ,--------(2分)
,--------(2分)
同样能使△ABE、△CDE与△BCE都相似.
得△ABD∽△BDC,则
 ,---------------------(2分)
,---------------------(2分)∴
 ,-----------------------------------------(1分)
,-----------------------------------------(1分)则
 .------------------------------(1分)
.------------------------------(1分)(2)作BH⊥DC,H为垂足,
则∠ABE+∠EBH=
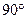 , ∠EBH+∠HBC=
, ∠EBH+∠HBC=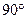 ,
,∴∠HBC=∠ABE,又∠BHC=∠A=
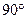 ,
,∴△ABE∽△HBC,------------------------------------(2分)
又AB‖CD,得HB=AD=x,HC=
 ,
,∴
 ,即
,即 ,--------------------------(2分)
,--------------------------(2分)解得
 ,定义域为
,定义域为 .----------------------(1分)
.----------------------(1分)(3)假设能使△ABE、△CDE与△BCE都相似,当点E在边AD上时,(如图1)

易知∠EBC=∠A=∠D=
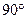 ,
,考虑∠1的对应角,容易得到∠1
 ,∠1
,∠1 ,
,所以必有∠1=∠2=∠3=
 ,
,于是在△ABE、△CDE中,易得
 ,
, ,
,∴
 ,------------------------------------------(2分)
,------------------------------------------(2分)
此时,
 ,
, , BC="6," ----------------
, BC="6," ---------------- -(1分)
-(1分)即能使△ABE、△CDE与△BCE都相似;当点E在边AD的延长线上时,(如图2)

类似分析可得∠1=∠2=∠3=
 ,可求得
,可求得 ,--------(2分)
,--------(2分)同样能使△ABE、△CDE与△BCE都相似.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 中,
中, 为
为 上一点,且
上一点,且 .
. 为等腰直角三角形,斜边
为等腰直角三角形,斜边 与
与 交于点
交于点 ,延长
,延长 ,连接
,连接 、
、 ,作
,作 ,垂足为
,垂足为 ,下列结论:①
,下列结论:① ≌
≌ ;②
;② 为等腰直角三角形;③
为等腰直角三角形;③ ;④
;④ ;⑤
;⑤ .其中正确的个数为( )
.其中正确的个数为( )


 中,
中, ∥
∥ ,点
,点 在
在 上,点
上,点 在
在 上,
上, 是中位线,若
是中位线,若 ,
, ,则用
,则用 、
、 表示
表示 _______
_______
 ,
, ,坝高DE=6米.
,坝高DE=6米.
 中,
中, ,
, ,
, ,在
,在 上截取
上截取 ,使
,使 ,过点
,过点 作
作 于
于 于点
于点 ,连接
,连接 ,交
,交 于点
于点 ,交
,交
 。
。

 ,
, ,求
,求