ƒøƒĞ»ı
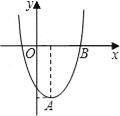
°æƒø°ø»ÁÕº1£¨‘Ğ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“—÷™µ„A£®0£¨4![]() £©£¨µ„B‘Ğx’˝∞Î÷·…œ£¨«“°œABO=30∂»£Æ∂ص„P‘Ğœş∂ŒAB…œ¥”µ„AœÚµ„B“‘√ø√Î
£©£¨µ„B‘Ğx’˝∞Î÷·…œ£¨«“°œABO=30∂»£Æ∂ص„P‘Ğœş∂ŒAB…œ¥”µ„AœÚµ„B“‘√ø√Î![]() ∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™t√ΣƑĞx÷·…œ»°¡Ωµ„M£¨N◊˜µ»±ş°˜PMN£Æ
∏ˆµ•ŒªµƒÀŸ∂»‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™t√ΣƑĞx÷·…œ»°¡Ωµ„M£¨N◊˜µ»±ş°˜PMN£Æ
£®1£©«Û÷±œşABµƒΩ‚Œˆ Ω£ª
£®2£©«Ûµ»±ş°˜PMNµƒ±ş≥§£®”√tµƒ¥˙ ˝ Ω±Ì æ£©£¨≤¢«Û≥ˆµ±µ»±ş°˜PMNµƒ∂•µ„M‘À∂ØµΩ”Î‘≠µ„O÷ÿ∫œ ±tµƒ÷µ£ª
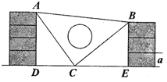
£®3£©»Áπ˚»°OBµƒ÷–µ„D£¨“‘ODŒ™±ş‘ĞRt°˜AOBƒĞ≤ø◊˜»ÁÕº2À˘ 浃æÿ–ŒODCE£¨µ„C‘Ğœş∂ŒAB…œ£Æ…˵»±ş°˜PMN∫Õæÿ–ŒODCE÷ÿµ˛≤ø∑÷µƒ√ʪ˝Œ™S£¨«Î«Û≥ˆµ±0°İt°İ2√Î ±S”Îtµƒ∫Ø ˝πÿœµ Ω£¨≤¢«Û≥ˆSµƒ◊Ó¥Û÷µ£Æ

°æ¥∞∏°ø(1) y=©Å![]() x+4
x+4![]() (2) PM=8©Åt£¨t=2 (3)µ±0°İt°İ1 ±£¨S=2
(2) PM=8©Åt£¨t=2 (3)µ±0°İt°İ1 ±£¨S=2![]() t+6
t+6![]() £ªµ±1£ºt£º2 ±£¨S=©Å2
£ªµ±1£ºt£º2 ±£¨S=©Å2![]() t2+6
t2+6![]() t+4
t+4![]() £ªµ±t=2 ±£¨S=8
£ªµ±t=2 ±£¨S=8![]() £ª◊Ó¥Û÷µŒ™
£ª◊Ó¥Û÷µŒ™![]()
°æΩ‚Œˆ°ø
£®1£©∏˘æı“—÷™Ãº˛«Ûµ√µ„Bµƒ◊¯±Í£¨‘Ÿ”√¥˝∂®œµ ˝∑®«Û÷±œşABµ√Ω‚Œˆ Ωº¥ø…£ª£®2£©‘ĞRt°˜AOB÷–£¨«Ûµ√AB=8![]() £¨º¥ø…±Ì æ≥ˆBP= 8
£¨º¥ø…±Ì æ≥ˆBP= 8![]() -
-![]() t£¨‘Ÿ”…tan°œPBM=
t£¨‘Ÿ”…tan°œPBM=![]() £¨º¥ø…”√tµƒ¥˙ ˝ Ω±Ì æPMµ√≥§£ªµ±µ„M”ε„O÷ÿ∫œ ±£¨ø…µ√AO=2AP£¨”…¥Àº¥ø…«Ûµ√t÷µ£ª£®3£©∏˘æıµ±0°İt°İ1 ±°¢µ±1£ºt£º2 ±º∞µ±t=2 ±£¨∑÷±«Û≥ˆS”Îtµƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢«Ûµ√◊Ó¥Û÷µ£¨±»Ωœº¥ø….
£¨º¥ø…”√tµƒ¥˙ ˝ Ω±Ì æPMµ√≥§£ªµ±µ„M”ε„O÷ÿ∫œ ±£¨ø…µ√AO=2AP£¨”…¥Àº¥ø…«Ûµ√t÷µ£ª£®3£©∏˘æıµ±0°İt°İ1 ±°¢µ±1£ºt£º2 ±º∞µ±t=2 ±£¨∑÷±«Û≥ˆS”Îtµƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢«Ûµ√◊Ó¥Û÷µ£¨±»Ωœº¥ø….
£®1£©”…OA=4![]() £¨°œABO=30°„£¨µ√µΩOB=12£¨
£¨°œABO=30°„£¨µ√µΩOB=12£¨
°‡B£®12£¨0£©£¨…Ë÷±œşABΩ‚Œˆ ΩŒ™y=kx+b£¨
∞—A∫ÕB◊¯±Í¥˙»Îµ√£∫![]() £¨
£¨
Ω‚µ√£∫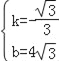 £¨
£¨
‘Ú÷±œşABµƒΩ‚Œˆ ΩŒ™£∫y=©Å![]() x+4
x+4![]() £Æ
£Æ
£®2£©°ş°œAOB=90°„£¨°œABO=30°„£¨
°‡AB=2OA=8![]() £¨
£¨
°şAP=![]() t£¨
t£¨
°‡BP=AB©ÅAP=8![]() t£¨
t£¨
°ş°˜PMN «µ»±ş»˝Ω«–Œ£¨
°‡°œMPB=90°„£¨
°ştan°œPBM=![]() £¨
£¨
°‡PM=£®8![]() ©Å
©Å![]() t£©°¡
t£©°¡![]() =8©Åt£Æ
=8©Åt£Æ
»ÁÕº1£¨π˝P∑÷±◊˜PQ°Õy÷·”ĞQ£¨PS°Õx÷·”ĞS£¨
ø…«Ûµ√AQ=![]() AP=
AP=![]() t£¨PS=QO=4
t£¨PS=QO=4![]() ©Å
©Å![]() t£¨
t£¨
°‡PM=£®4![]() ©Å
©Å![]() £©°¬
£©°¬![]() =8©Åt£¨
=8©Åt£¨
µ±µ„M”ε„O÷ÿ∫œ ±£¨
°ş°œBAO=60°„£¨
°‡AO=2AP£Æ
°‡4![]() =2
=2![]() t£¨
t£¨
°‡t=2£Æ

£®3£©¢Ÿµ±0°İt°İ1 ±£¨º˚Õº2£Æ
…ËPNΩªEC”е„G£¨÷ÿµ˛≤ø∑÷Œ™÷±Ω«Ãı–ŒEONG£¨◊˜GH°ÕOB”ĞH£Æ
°ş°œGNH=60°„£¨![]() £¨
£¨
°‡HN=2£¨
°şPM=8©Åt£¨
°‡BM=16©Å2t£¨
°şOB=12£¨
°‡ON=£®8©Åt£©©Å£®16©Å2t©Å12£©=4+t£¨
°‡OH=ON©ÅHN=4+t©Å2=2+t=EG£¨
°‡S=![]() £®2+t+4+t£©°¡2
£®2+t+4+t£©°¡2![]() =2
=2![]() t+6
t+6![]() £Æ
£Æ
°şSÀÊtµƒ‘ˆ¥Û∂¯‘ˆ¥Û£¨
°‡µ±t=1 ±£¨Smax=8![]() £Æ
£Æ
¢Ğµ±1£ºt£º2 ±£¨º˚Õº3£Æ
…ËPMΩªEC”е„I£¨ΩªEO”е„F£¨PNΩªEC”е„G£¨÷ÿµ˛≤ø∑÷Œ™ŒÂ±ş–ŒOFIGN£Æ
◊˜GH°ÕOB”ĞH£¨
°şFO=4![]() ©Å2
©Å2![]() t£¨
t£¨
°‡EF=2![]() ©Å£®4
©Å£®4![]() ©Å2
©Å2![]() t£©=2
t£©=2![]() t©Å2
t©Å2![]() £¨
£¨
°‡EI=2t©Å2£Æ
°‡S=SÃı–ŒONGE©ÅS°˜FEI=2![]() t+6
t+6![]() ©Å
©Å![]() £®2t©Å2£©£®2
£®2t©Å2£©£®2![]() t©Å2
t©Å2![]() £©=©Å2
£©=©Å2![]() t2+6
t2+6![]() t+4
t+4![]()
”…“‚ø…µ√MO=4©Å2t£¨OF=£®4©Å2t£©°¡![]() £¨PC=4
£¨PC=4![]() ©Å
©Å![]() t£¨PI=4©Åt£¨
t£¨PI=4©Åt£¨
‘Ÿº∆À„S°˜FMO=![]() £®4©Å2t£©2°¡
£®4©Å2t£©2°¡![]()
S°˜PMN=![]() £®8©Åt£©2£¨S°˜PIG=
£®8©Åt£©2£¨S°˜PIG=![]() £®4©Åt£©2£¨
£®4©Åt£©2£¨
°‡S=S°˜PMN©ÅS°˜PIG©ÅS°˜FMO=![]() £®8©Åt£©2©Å
£®8©Åt£©2©Å![]() £®4©Åt£©2©Å
£®4©Åt£©2©Å![]() £®4©Å2t£©2°¡
£®4©Å2t£©2°¡![]()
=©Å2![]() t2+6
t2+6![]() t+4
t+4![]()
°ş©Å2![]() £º0£¨
£º0£¨
°‡µ±![]() ±£¨S”–◊Ó¥Û÷µ£¨Smax=
±£¨S”–◊Ó¥Û÷µ£¨Smax=![]() £Æ
£Æ
¢ğµ±t=2 ±£¨MP=MN=6£¨º¥N”ÎD÷ÿ∫œ£¨
…ËPMΩªEC”е„I£¨PDΩªEC”е„G£¨÷ÿµ˛≤ø
∑÷Œ™µ»—¸Ãı–ŒIMNG£¨º˚Õº4£ÆS=![]() °¡62©Å
°¡62©Å![]() °¡22=8
°¡22=8![]() £¨
£¨
◊ğ…œÀ˘ ˆ£∫µ±0°İt°İ1 ±£¨S=2![]() t+6
t+6![]() £ª
£ª
µ±1£ºt£º2 ±£¨S=©Å2![]() t2+6
t2+6![]() t+4
t+4![]() £ª
£ª
µ±t=2 ±£¨S=8![]() £Æ
£Æ

°ş![]() £¨
£¨
°‡Sµƒ◊Ó¥Û÷µ « ![]() £Æ
£Æ