题目内容
如图,在梯形 中,
中,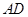 ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.

(1)求证: ;
;
(2)当 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由.
 中,
中,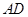 ∥
∥ ,
, ,
, ,点
,点 在对角线
在对角线 上,作
上,作 ,连接
,连接 ,且满足
,且满足 .
.
(1)求证:
 ;
;(2)当
 时,试判断四边形
时,试判断四边形 的形状,并说明理由.
的形状,并说明理由.见解析
证明:(1)∵ ,
,
∴ (1分)
(1分)
∵ ,
,
∴ ≌
≌ (1分)
(1分)
∴ (1分)
(1分)
∵ ,
,
∴ (1分)
(1分)
∴ ,
,
∴ (1分)
(1分)
∴ (1分)
(1分)
(2)四边形 是正方形 (1分)
是正方形 (1分)
∵ ,
,
∴ ,
,
∴ (2分)
(2分)
∵
∴ ∽
∽ (1分)
(1分)
∴ (1分)
(1分)
∵ ,
,
∴四边形 是矩形 (1分)
是矩形 (1分)
∵ ,
,
∴四边形 是正方形
是正方形
(1)利用互余关系证明∠BCE=∠DCF,又有BC=DC,EC=CF,可证△BCE≌△DCF,得出∠EBC=∠FDC,由已知可知△BCD为等腰直角三角形,故有∠BDC=∠EBC=∠FDC=45°,可证∠FDB=90°,证明BD⊥DF;
(2)四边形DECF是正方形.由BC2=DE•DB及BC=DC,得DC2=DE•DB,转化为比例式,利用公共角∠CDE=∠BDC,证明△CDE∽△BDC,则有∠DEC=∠DCB=90°,判断四边形DECF是矩形,结合条件CE=CF,可证四边形DECF是正方形.
 ,
, ∴
 (1分)
(1分)∵
 ,
,∴
 ≌
≌ (1分)
(1分)∴
 (1分)
(1分)∵
 ,
,∴
 (1分)
(1分)∴
 ,
,∴
 (1分)
(1分)∴
 (1分)
(1分)(2)四边形
 是正方形 (1分)
是正方形 (1分)∵
 ,
,∴
 ,
, ∴
 (2分)
(2分)∵

∴
 ∽
∽ (1分)
(1分)∴
 (1分)
(1分)∵
 ,
, ∴四边形
 是矩形 (1分)
是矩形 (1分)∵
 ,
, ∴四边形
 是正方形
是正方形(1)利用互余关系证明∠BCE=∠DCF,又有BC=DC,EC=CF,可证△BCE≌△DCF,得出∠EBC=∠FDC,由已知可知△BCD为等腰直角三角形,故有∠BDC=∠EBC=∠FDC=45°,可证∠FDB=90°,证明BD⊥DF;
(2)四边形DECF是正方形.由BC2=DE•DB及BC=DC,得DC2=DE•DB,转化为比例式,利用公共角∠CDE=∠BDC,证明△CDE∽△BDC,则有∠DEC=∠DCB=90°,判断四边形DECF是矩形,结合条件CE=CF,可证四边形DECF是正方形.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 中,
中, ,
, 的平分线交
的平分线交 于
于 ,
, ,垂足为
,垂足为 ,连结
,连结 ,交
,交 于点
于点 .
. 
 ;
; ∥
∥ ,连结
,连结 ,猜想四边形
,猜想四边形 是什么图形?并证明你的猜想.
是什么图形?并证明你的猜想.
 的形状,并说明理由;
的形状,并说明理由;

 ,它的周长是
,它的周长是 ,则它的中位线长为
,则它的中位线长为  .
. 沿着折痕
沿着折痕 折叠,使点
折叠,使点 落在边
落在边 的中点
的中点 处,那么四边形
处,那么四边形 的面积等于 .
的面积等于 .

