Question

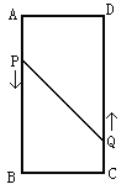
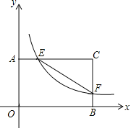
【题目】如图，四边形是矩形，为原点，、的坐标分别为、，是边上的一个动点（不与，重合），过点的反比例函数的图象与边交于点．

当时，写出点、的坐标；

求的值；

是否存在这样的点，使得将沿对折后，点恰好落在上？若存在，求出此时点的坐标；若不存在，请说明理由．

Answer 1

【答案】(1)，；(2)；(3) 存在符合条件的点，它的坐标为．

【解析】

（1）根据题意可知E的纵坐标为4，F的横坐标为6，分别代入y=，即可求得E、F的坐标；

（2）根据反比例函数的性质得出，xy=k，即可得出AEAO=BFBO，从而得出，进而求得；

（3）设折叠之后C点在OB上的对称点为C'，连接C'E、C'F，过E作EG垂直于OB于点G，则根据折叠性质、相似三角形、勾股定理得出即可．

解：当时，则，

∵反比例函数的图象经过点、，

∵、的坐标分别为、，

∴的纵坐标为，的横坐标为，

∴，；

∵根据反比例函数的性质得出，，

∴，

∴，

∵，，

∴，

∴，

∴，

∴；

设存在这样的点，将沿对折后，点恰好落在边上的点，

过点作，垂足为．

由题意得：，

把代入得：，把代入得：，

∴，，

∵，

∴．

又∵，

∴．

∴，

∴：：，

∴，

∵，

∴，

解得，

∴，

∴存在符合条件的点，它的坐标为．