题目内容
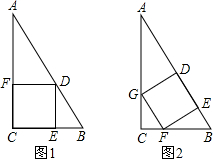
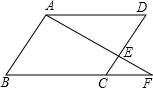
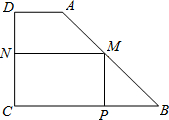
如图，有右块形状是直角梯形的铁皮ABCD，上底AD=3cm，下底BC=六cm，垂直于底的腰CD=6cm．现要截成右矩形铁皮MPCN，使它的顶点M、P、N在AB、BC、CD上，设MN的长为x，矩形MPCN的面积为m．
（1）求m与x之间的关系式，并指出x的取值范围．
（2）当x为何值时，矩形MPCN的面积最大？最大面积是八少？
（1）求m与x之间的关系式，并指出x的取值范围．
（2）当x为何值时，矩形MPCN的面积最大？最大面积是八少？
（4）过A作3C的垂线，垂足是E．
又∵x0⊥3C
∴AE∥x0
∴△AE3∽△x03
∴
=
即
=
，解得：x0=
则y=x（
）=-
x4+
x （3＜x≤6）；
（4）∵y=-
x4+
x=-
（x4-8x+46-46）=-
（x-4）4+
，
∴当x=4时，有最大面积为：
．
又∵x0⊥3C
∴AE∥x0
∴△AE3∽△x03
∴
| AE |
| x0 |
| 3E |
| 03 |
即
| 6 |
| x0 |
| 5 |
| 8-x |
| 48-6x |
| 5 |
则y=x（
| 48-6x |
| 5 |
| 6 |
| 5 |
| 48 |
| 5 |
（4）∵y=-
| 6 |
| 5 |
| 48 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 76 |
| 5 |
∴当x=4时，有最大面积为：
| 76 |
| 5 |
练习册系列答案
口算题天天练系列答案
相关题目
