题目内容
【题目】在一条直线上依次有![]() 、
、![]() 、
、![]() 三个港口,甲、乙两船同时分别从
三个港口,甲、乙两船同时分别从![]() 、
、![]() 港口出发,沿直线匀速驶向
港口出发,沿直线匀速驶向![]() 港,最终达到
港,最终达到![]() 港.设甲、乙两船行驶
港.设甲、乙两船行驶![]() 后,与
后,与![]() 港的距离分别为
港的距离分别为![]() 、
、![]() ,
,![]() 、
、![]() 与
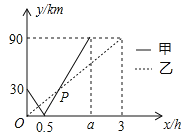
与![]() 的函数关系如图所示.
的函数关系如图所示.
(![]() )填空:
)填空:![]() 、
、![]() 两港口间的距离为__________
两港口间的距离为__________![]() ,
,![]() __________.
__________.
(![]() )求图中点
)求图中点![]() 的坐标.
的坐标.
(![]() )若两船的距离不超过
)若两船的距离不超过![]() 时能够相互望见,求甲、乙两船可以相互望见时
时能够相互望见,求甲、乙两船可以相互望见时![]() 的取值范围.
的取值范围.
【答案】(![]() )
)![]() ,
,![]() (
(![]() )
)![]() (
(![]() )
)![]() 或
或![]()
【解析】试题分析:
(1)由题意和图中信息可知:①A、C两港口相距30+90=120(km);②甲船从A到B用0.5小时行驶了30km,从B到C用(a-0.5)小时行驶了90km,根据甲船行驶速度始终保持不变即可列出方程求得a的值;
(2)根据图中信息分别求得y1和y2在![]() 时的解析式,由在P点处y1=y2即可列出方程求得对应的x的值,进而可求得对应的y的值即可得到点P的坐标;
时的解析式,由在P点处y1=y2即可列出方程求得对应的x的值,进而可求得对应的y的值即可得到点P的坐标;
(3)根据题意和图象分以下4种情况求得对应的x的值:①当![]() ,两船间的距离小等于10km;②当
,两船间的距离小等于10km;②当![]() 时,两船间的距离等于10km;③当
时,两船间的距离等于10km;③当![]() 时,两船间的距离等于10km;④当
时,两船间的距离等于10km;④当![]() 时,两船间的距离等于10km;这样结合题意即可得到两船间的距离小于或等于10km时所对应的x的取值范围了.
时,两船间的距离等于10km;这样结合题意即可得到两船间的距离小于或等于10km时所对应的x的取值范围了.
试题解析:
(![]() )
)![]() 、
、![]() 两港口距离
两港口距离![]() ,
,
∵ 甲船行驶速度不变,
∴ ![]() ,
,
∴ ![]() .
.
(![]() )由点
)由点![]() 求得:
求得:![]() ,
,
当![]() 时,由点
时,由点![]() ,
,![]() ,
,
求得:![]() ,
,
当![]() 时,
时,![]() ,
,
∴ ![]() ,
,
此时,![]() ,
,
∴ ![]() 点坐标
点坐标![]() .
.
(![]() )①当
)①当![]() 时,由点
时,由点![]() ,
,![]() ,
,
可得:![]() ,
,
由:![]() ,解得:
,解得:![]() ,不符合题意.
,不符合题意.
②当![]() 时,
时,
![]() ,
,
得:![]() ,
,
∴ ![]() ;
;
③当![]() 时,
时,
![]() ,
,
得:![]() ,
,
∴ ![]() ;
;
④当![]() 时,甲船已经到了,而乙船正在行驶,
时,甲船已经到了,而乙船正在行驶,
∴ ![]() ,
,
得:![]() ,
,
∴ ![]() ,
,
∴ 综上所述,当![]() 或
或![]() 时,甲、乙两船可以互相望见.
时,甲、乙两船可以互相望见.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批 粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的 粒数m | 96 | 282 | 382 | 570 | 948 | 1912 | 2850 |
发芽的 频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.956 | 0.950 |
则绿豆发芽的概率估计值是( )
A. 0.96 B. 0.95 C. 0.94 D. 0.90