题目内容
如图,直线y=
x+1分别与两坐标轴交于A,B两点,点C从A点出发沿射线BA方向移动,速度为每秒1个单位长度.以C为顶点作等边△CDE,其中点D和点E都在x轴上.半径为3
-3的⊙M与x轴、直线AB相切于点G、F.
(1)直线AB与x轴所夹的角∠ABO=
(2)求当点C移动多少秒时,等边△CDE的边CE与⊙M相切?

| ||
| 3 |
| 3 |
(1)直线AB与x轴所夹的角∠ABO=
30°
30°
°;(2)求当点C移动多少秒时,等边△CDE的边CE与⊙M相切?

分析:(1)根据直线解析式求出OA、OB的长度,再由∠ABO的正切值,可求出∠AOB的度数.
(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
(2)设点C移动t秒后与⊙M相切,分两种情况讨论,①当CE在⊙M左侧相切于点H;②当CE在⊙M右侧相切于点H,用含t的式子表示出CE,建立方程,解出即可得出答案.
解答: 解:(1)直线AB的解析式为y=
解:(1)直线AB的解析式为y=
x+1,
令x=0,则y=1,令y=0,则x=-
,
∵tan∠ABO=
=
=
,
∴∠ABO=30°;
(2)设点C移动t秒后与⊙M相切,
①当CE在⊙M左侧相切于点H,
连接MF、MG、MH,
∵AB、CE、BO均为⊙M的切线,
∴MF⊥AB,MH⊥CE,MG⊥BO,
∵∠ABO=30°,△CDE是等边三角形,
∴∠BCE=90°,
∴四边形CHMF为矩形,
∵MF=MH,
∴四边形CHMF为正方形,
∴CH=MH=3
-3,
∵EH、EG为⊙M的切线,∠CED=60°,
∴∠HEM=60°,
∴HE=
MH=3-
,
∵CE=
BC=
(2+t),
∴
(2+t)=3
-3+3-
,
∴t=4;
 ②当CE在⊙M右侧相切于点H,
②当CE在⊙M右侧相切于点H,
由①证得:CH=MH=3
-3,
∵∠HEM=30°,
∴HE=
MH=9-3
,
∴
(2+t)=3
-3+9-3
,
∴t=6
-2.
 解:(1)直线AB的解析式为y=
解:(1)直线AB的解析式为y=
| ||
| 3 |
令x=0,则y=1,令y=0,则x=-
| 3 |
∵tan∠ABO=
| OA |
| OB |
| 1 | ||
|
| ||
| 3 |
∴∠ABO=30°;
(2)设点C移动t秒后与⊙M相切,
①当CE在⊙M左侧相切于点H,
连接MF、MG、MH,
∵AB、CE、BO均为⊙M的切线,
∴MF⊥AB,MH⊥CE,MG⊥BO,
∵∠ABO=30°,△CDE是等边三角形,

∴∠BCE=90°,
∴四边形CHMF为矩形,
∵MF=MH,
∴四边形CHMF为正方形,
∴CH=MH=3
| 3 |
∵EH、EG为⊙M的切线,∠CED=60°,
∴∠HEM=60°,
∴HE=
| 1 | ||
|
| 3 |
∵CE=
| 1 | ||
|
| 1 | ||
|
∴
| 1 | ||
|
| 3 |
| 3 |
∴t=4;
 ②当CE在⊙M右侧相切于点H,
②当CE在⊙M右侧相切于点H,由①证得:CH=MH=3
| 3 |
∵∠HEM=30°,
∴HE=
| 3 |
| 3 |
∴
| 1 | ||
|
| 3 |
| 3 |
∴t=6
| 3 |
点评:本题考查了圆的综合,涉及了切线的性质、等边三角形的性质、特殊角的三角函数值解答本题的关键是数形结合思想及分类讨论思想的综合运用,难度较大.

练习册系列答案
相关题目
 正△ABC.
正△ABC.
 如图,直线y=-
如图,直线y=- (2012•黄埔区一模)如图,直线
(2012•黄埔区一模)如图,直线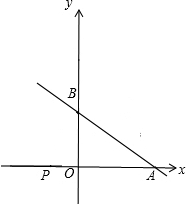 B沿直线AB翻折得到△CAB,点C恰好为经过点A的抛物线的顶点.
B沿直线AB翻折得到△CAB,点C恰好为经过点A的抛物线的顶点.