题目内容

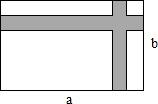
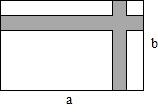
已知一个矩形的两条对角线夹角为60°，一条对角线的长为10cm，则该矩形的周长为

A.
20cm
B.
$数学公式$ cm
C.
$数学公式$ cm
D.
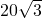$数学公式$ cm

D
分析：根据矩形的两条对角线的夹角为60°，可以判定△AOB为等边三角形，即可求得AB=AO，在直角△ABC中，已知AC，AB，根据勾股定理即可计算BC的长，进而计算矩形的周长即可解题．
解答：

解：矩形的两条对角线的夹角为∠1=60°，
且矩形对角线相等且互相平分，
∴△AOB为等边三角形，
∴AB=AO= $\text{[math]}$ AC=5，
在直角△ABC中，AC=10，AB=5，
∴BC= $\text{[math]}$ =5 $\text{[math]}$ ，
故矩形的周长为2BC+2AB=10 $\text{[math]}$ +10=10（1+ $\text{[math]}$ ）cm．
故选D．
点评：本题考查了矩形对角线相等且互相平分的性质，等边三角形的判定，勾股定理在直角三角形中的运用，本题中根据勾股定理计算BC的长是解题的关键．

练习册系列答案

英语首字母综合填空系列答案

英语奥林匹克系列答案

英才小状元系列答案

英才计划期末集中赢系列答案

银博士轻巧夺冠系列答案

一通百通考必赢系列答案

一线名师夺冠王检测卷系列答案

一线名师提优试卷系列答案

一路领先优选卷系列答案

一路领先口算题卡系列答案

相关题目

某中学有一块长为a米，宽为b米的矩形场地，计划在该场地上修筑宽都为2米的两条互相垂直的道路，余下的四块矩形小场地建成草坪．
（1）如图，请分别写出每条道路的面积（用含a或含b的代数式表示）；
（2）已知a：b=2：1，并且四块草坪的面积之和为312米²，试求原来矩形场地的长与宽各为多少米？
（3）在（2）的条件下，为进一步美化校园，根据实际情况，学校决定对整个矩形场地作如下设计（要求同时符合下述两个条件）：
条件①：在每块草坪上各修建一个面积尽可能大的菱形花圃（花圃各边必须分别与所在草坪的对角线平行），并且其中有两个花圃的面积之差为13米²；
条件②：整个矩形场地（包括道路、草坪、花圃）为轴对称图形．
请你画出符合上述设计方案的一种草图（不必说明画法与根据），并求出每个菱形花圃的面积．

某中学有一块长为a米，宽为b米的矩形场地，计划在该场地上修筑宽都为2米的两条互相垂直的道路，余下的四块矩形小场地建成草坪．
（1）如图，请分别写出每条道路的面积（用含a或含b的代数式表示）；
（2）已知a：b=2：1，并且四块草坪的面积之和为312米²，试求原来矩形场地的长与宽各为多少米？
（3）在（2）的条件下，为进一步美化校园，根据实际情况，学校决定对整个矩形场地作如下设计（要求同时符合下述两个条件）：
条件①：在每块草坪上各修建一个面积尽可能大的菱形花圃（花圃各边必须分别与所在草坪的对角线平行），并且其中有两个花圃的面积之差为13米²；
条件②：整个矩形场地（包括道路、草坪、花圃）为轴对称图形．
请你画出符合上述设计方案的一种草图（不必说明画法与根据），并求出每个菱形花圃的面积．

（2002•泉州）某中学有一块长为a米，宽为b米的矩形场地，计划在该场地上修筑宽都为2米的两条互相垂直的道路，余下的四块矩形小场地建成草坪．
（1）如图，请分别写出每条道路的面积（用含a或含b的代数式表示）；
（2）已知a：b=2：1，并且四块草坪的面积之和为312米²，试求原来矩形场地的长与宽各为多少米？
（3）在（2）的条件下，为进一步美化校园，根据实际情况，学校决定对整个矩形场地作如下设计（要求同时符合下述两个条件）：
条件①：在每块草坪上各修建一个面积尽可能大的菱形花圃（花圃各边必须分别与所在草坪的对角线平行），并且其中有两个花圃的面积之差为13米²；
条件②：整个矩形场地（包括道路、草坪、花圃）为轴对称图形．
请你画出符合上述设计方案的一种草图（不必说明画法与根据），并求出每个菱形花圃的面积．

已知从矩形的一个顶点向其所对的对角线引垂线，该垂线分直角为 3：1 的两部分. 则该垂线与另一条对角线的夹角是

A.60°
B.45°
C.30°
D.22.5°

已知从矩形的一个顶点向其所对的对角线引垂线，该垂线分直角为 3：1两部分，则该垂线与另一条对角线的夹角是

A.60°
B. 45°
C. 30°
D. 22.5°