题目内容
已知E为?ABCD内任一点，?ABCD的面积为40，那么S△EAB+S△ECD= ．
【答案】分析：过E作直线MN⊥AB，则MN⊥CD，根据S△EAB+S△ECD=
AB•EM+
CD•EN=
AB（EM+EN）=
AB•MN=
S?ABCD即可求解．
解答：解：过E作直线MN⊥AB，则MN⊥CD，
S△EAB=
AB•EM，S△ECD=
CD•EN．
S△EAB+S△ECD=
AB•EM+
CD•EN=
AB（EM+EN）=
AB•MN=
S?ABCD=20．
故答案是：20．
点评：本题主要考查了平行四边形的性质，正确理解S△EAB+S△ECD=
AB•EM+
CD•EN=
AB（EM+EN）=
AB•MN=
S?ABCD是解题的关键．
AB•EM+CD•EN=AB（EM+EN）=AB•MN=S?ABCD即可求解．解答：解：过E作直线MN⊥AB，则MN⊥CD，
S△EAB=
AB•EM，S△ECD=CD•EN．S△EAB+S△ECD=
AB•EM+CD•EN=AB（EM+EN）=AB•MN=S?ABCD=20．故答案是：20．
点评：本题主要考查了平行四边形的性质，正确理解S△EAB+S△ECD=
AB•EM+CD•EN=AB（EM+EN）=AB•MN=S?ABCD是解题的关键． 
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
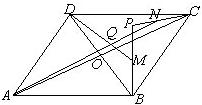17、已知P为?ABCD内一点，O为AC与BD的交点，M、N分别为PB，PC的中点，Q为AN与DM的交点，
已知P为?ABCD内一点，O为AC与BD的交点，M、N分别为PB，PC的中点，Q为AN与DM的交点，