题目内容
如图,已知在⊙O中,AB=4 ,AC是⊙O的直径,AC⊥BD于F,∠A=30°.图中阴影部分的面积是( )
,AC是⊙O的直径,AC⊥BD于F,∠A=30°.图中阴影部分的面积是( )
A.4π
B.π
C.

D.

【答案】分析:由∠A=30°,可求得∠BOC=60°,再根据垂径定理得∠BOD=120°,由勾股定理得出BF以及OB的长,从而计算出阴影部分的面积即扇形的面积.
解答: 解:∵AC⊥BD于F,∠A=30°,
解:∵AC⊥BD于F,∠A=30°,
∴∠BOC=60°(在同圆中,同弧所对的圆周角是所对的圆心角的一半),
∴∠OBF=30°(直角三角形的两个锐角互余),
∵AB=4 ,
,
∴BF=2 ,
,
∵sin∠BOF=sin60°= ,
,
∴ =
= ,
,
∴OB=4,
∴S阴影=S扇形= =
= π.
π.
故选D.
点评:本题考查了扇形面积的计算,以及圆周角定理、垂径定理和勾股定理,是基础知识要熟练掌握.
解答:
 解:∵AC⊥BD于F,∠A=30°,
解:∵AC⊥BD于F,∠A=30°,∴∠BOC=60°(在同圆中,同弧所对的圆周角是所对的圆心角的一半),
∴∠OBF=30°(直角三角形的两个锐角互余),
∵AB=4
 ,
,∴BF=2
 ,
,∵sin∠BOF=sin60°=
 ,
,∴
 =
= ,
,∴OB=4,
∴S阴影=S扇形=
 =
= π.
π.故选D.
点评:本题考查了扇形面积的计算,以及圆周角定理、垂径定理和勾股定理,是基础知识要熟练掌握.

练习册系列答案
相关题目
 20、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.
20、如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.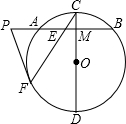 作⊙O的切线交BA的延长线于点P.
作⊙O的切线交BA的延长线于点P. (2011•普宁市一模)如图,已知在?ABCD中,E、F是对角线BD延长线上的两点,且∠BCE=∠DAF,求证:△ECD≌△FAB.
(2011•普宁市一模)如图,已知在?ABCD中,E、F是对角线BD延长线上的两点,且∠BCE=∠DAF,求证:△ECD≌△FAB. 如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.
如图,已知在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,CE的垂直平分线正好经过点B,与AC相交于点F,求∠A的度数.