题目内容
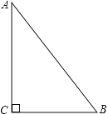
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm,若动点P从点C开始,沿C→A→B→C的路径运动一周,且速度为每秒2cm,设运动时间为t秒,当t=_____时,点P与△ABC的某两个顶点构成等腰三角形.
【答案】4或![]() 或
或![]() 或
或![]() 或3或
或3或![]() .
.
【解析】
分点P在边AC和边AB上讨论: 当点P在边AC上时和当点P在边AB上时,进行计算即可得到答案.
∵△ABC中,∠C=90°,AC=4cm,BC=3cm,
∴AB=![]() =
=![]() =5,
=5,
当点P在边AC上时,当PA=PB时,如图1,
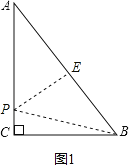
作AB边上的高PE,则AE=BE=![]() ,
,
易证得△APE∽△ABC,
∴![]() ,即
,即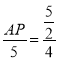 ,
,
∴AP=![]() ,
,
此时(4﹣![]() )÷2=
)÷2=![]() (秒);
(秒);
当CP=CB时,
∵CP=3cm,此时t=3÷2=![]() (秒);
(秒);
当点P在边AB上时,
当AC=AP,此时(4+4)÷2=4(秒);
当AP=PC时,如图2,
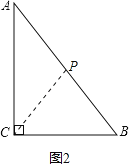
∴点P在AC的垂直平分线与AB的交点处,即在AB的中点,
则AP=![]() AB=
AB=![]() ,此时(4+2.5)÷2=
,此时(4+2.5)÷2=![]() (秒)
(秒)
当CP=CB时,如图3,
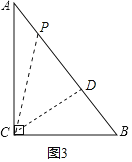
作AB边上的高CD,
∵![]() AC×BC=
AC×BC=![]() AB×CD.
AB×CD.
∴CD=![]() =
=![]() ,
,
在Rt△CDP中,根据勾股定理得,DP=![]() =1.8,
=1.8,
∴BP=2DP=3.6,
∴AP=1.4,
∴t=(AC+AP)÷2=(4+1.4)÷2=![]() (秒)
(秒)
当BC=BP时,
∴BP=3cm,CA+AP=4+5﹣3=6(cm),
∴t=6÷2=3(秒);
当PB=PC,
∴点P在BC的垂直平分线与AB的交点处,即在AB的中点,
此时CA+AP=4+2.5=6.5(cm),
t=6.5÷2=![]() (秒);
(秒);
综上可知,当4或![]() 或
或![]() 或
或![]() 或3或
或3或![]() 时点P与△ABC的某两个顶点构成等腰三角形,故答案为4或
时点P与△ABC的某两个顶点构成等腰三角形,故答案为4或![]() 或
或![]() 或
或![]() 或3或
或3或![]() .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目