题目内容
10.一个三角形的底边a增加了k,该边上的高h减少k后,若其面积保持不变,则a-h=-k.分析 根据三角形的面积公式列出原三角形的面积表达式和现在的三角形的面积表达式,由于三角形的面积不变,进而求出a-h.
解答 解:由题意得
$\frac{1}{2}$a•h=$\frac{1}{2}$(a+k)(h-k),
即ah=ah+kh-ah-k2,
k(h-a)=-k2.
h-a=-k.
故答案为:-k.
点评 本题主要考查了多项式乘多项式,用到的知识点是三角形的面积公式和多项式乘多项式的法则,根据三角形的面积公式列出等式,进而解答,此题需要同学们熟练掌握.

练习册系列答案
相关题目
18.已知a、b是有理数,观察表中的运算,并在空格内填上相应的数.
| a与b的运算 | a+2b | 2a+b | 3a+2b |
| 运算的结果 | 2 | 4 | 6 |
15.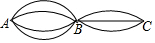 如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )
如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )
 如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )
如图,从A地到B地有4条路,从B地到C地也有3条路,则从A地到C地可供选择的方案有( )| A. | 3种 | B. | 4种 | C. | 7种 | D. | 12种 |
20.下列方程中是一元一次方程的是( )
| A. | 2x+y=3 | B. | 3x-1=0 | C. | $\frac{1}{x-2}=4$ | D. | 4x-1 |
 如图,在长方形ABCD中,AB=6cm,BC=8cm.动点P从点A出发,以3cm/s的速度沿逆时针方向匀速运动,当点P运动到点A时,运动停止.设点P运动的时间为t(s).
如图,在长方形ABCD中,AB=6cm,BC=8cm.动点P从点A出发,以3cm/s的速度沿逆时针方向匀速运动,当点P运动到点A时,运动停止.设点P运动的时间为t(s).