题目内容
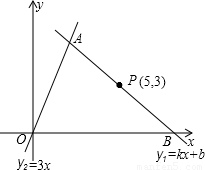
(2002•丽水)如图,直线y1=kx+b经过点P(5,3),且分别与已知直线y2=3x交于点A、与x轴交于点B.设点A的横坐标为m(m>1且m≠5).(1)用含m的代数式表示k;
(2)写出△AOB的面积S关于m的函数解析式;
(3)在直线y2=3x上是否存在点A,使得△AOB面积最小?若存在,请求出点A的坐标;若不存在,请说明理由.
【答案】分析:(1)由题意可得A点坐标,由斜率定义得斜率k;
(2)将P点坐标代入解析式得到m,再另y=o,得到点B坐标,然后可得到面积函数;
(3)由函数性质可得答案.
解答:解:(1)由题意得,A点坐标为(m,3m),
由斜率定义得,k= .
.
(2)所以y1= x+b,
x+b,
将P(5,3)代入直线方程解得,b= ,
,
令y1=0得,x= ,
,
SAOB= •
• •3m.
•3m.
(3)由(2)得,SAOB= ,当m趋近于无穷大时,有最小值6.
,当m趋近于无穷大时,有最小值6.
点评:本题涉及一次函数的综合应用,难度中上
(2)将P点坐标代入解析式得到m,再另y=o,得到点B坐标,然后可得到面积函数;
(3)由函数性质可得答案.
解答:解:(1)由题意得,A点坐标为(m,3m),
由斜率定义得,k=
 .
.(2)所以y1=
 x+b,
x+b,将P(5,3)代入直线方程解得,b=
 ,
,令y1=0得,x=
 ,
,SAOB=
 •
• •3m.
•3m.(3)由(2)得,SAOB=
 ,当m趋近于无穷大时,有最小值6.
,当m趋近于无穷大时,有最小值6.点评:本题涉及一次函数的综合应用,难度中上

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目