题目内容
(2014•张家口二模)已知⊙O及⊙O外一点P,过点P作出⊙O的一条切线(只有圆规和三角板这两种工具).以下是甲、乙两同学的作业:
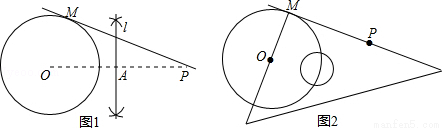
甲:①连接OP,作OP的垂直平分线l,交OP于点A;
②以点A为圆心、OA为半径画弧、交⊙O于点M;
③作直线PM,则直线PM即为所求(如图1).
乙:①让直角三角板的一条直角边始终经过点P;
②调整直角三角板的位置,让它的另一条直角边过圆心O,直角顶点落在⊙O上,记这时直角顶点的位置为点M;
③作直线PM,则直线PM即为所求(如图2).
对于两人的作业,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
C
【解析】
试题分析:(1)连接OM,OA,连接OP,作OP的垂直平分线l可得OA=MA=OP,进而得到∠O=∠AMO,∠AMP=∠MPA,所以∠OMA+∠AMP=∠O+∠MPA=90°,得出MP是⊙O的切线,
(2)直角三角板的一条直角边始终经过点P,它的另一条直角边过圆心O,直角顶点落在⊙O上,所以∠OMP=90°,得到MP是⊙O的切线.
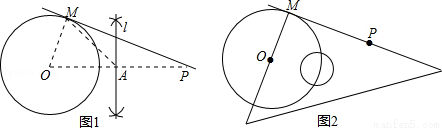
证明:如图1连接OM,OA,
∵连接OP,作OP的垂直平分线l,交OP于点A;
∴OA=OP,
∵以点A为圆心、OA为半径画弧、交⊙O于点M;
∴OA=MA=OP,
∴∠O=∠AMO,∠AMP=∠MPA,
∴∠OMA+∠AMP=∠O+∠MPA=90°
∴OM⊥MP,
∴MP是⊙O的切线,
(2)如图2
∵直角三角板的一条直角边始终经过点P,它的另一条直角边过圆心O,直角顶点落在⊙O上,
∴∠OMP=90°,
∴MP是⊙O的切线.
故两位同学的作法都正确,
故选:C.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 篮球队员在罚球线投篮2次,至少投中一次
篮球队员在罚球线投篮2次,至少投中一次
 是半圆.甲、乙两人想在
是半圆.甲、乙两人想在