题目内容
2. 如图,△ABC中,∠A=60°,∠C=20°,D是BC的中点,E是AC上一点,CD=CE,若S△ABC+2S△CDE=2$\sqrt{3}$,则AC=4.
如图,△ABC中,∠A=60°,∠C=20°,D是BC的中点,E是AC上一点,CD=CE,若S△ABC+2S△CDE=2$\sqrt{3}$,则AC=4.
分析 如图作CF⊥AB交AB的延长线于F,连接DF.由△BDF≌△ECD,推出S△CDE=S△BDF=S△DFC,推出S△AFC=2$\sqrt{3}$,设AF=a,则CF=$\sqrt{3}$a,推出$\frac{1}{2}$•a•$\sqrt{3}$a=2$\sqrt{3}$,求出a即可解决问题.
解答 解:如图作CF⊥AB交AB的延长线于F,连接DF.
∵∠A=60°,∠AFC=90°,
∴∠ACF=30°,
∵∠ACB=20°,
∴∠DCF=10°,
在Rt△BCF中,∵BD=DC,
∴DF=DB=DC,
∴∠DFC=∠DCF=10°,
∴∠BDF=∠DFC+∠DCF=20°,
在△DBF和△CED中,
$\left\{\begin{array}{l}{BD=CE}\\{∠BDF=∠ECD}\\{DF=CD}\end{array}\right.$,
∴△BDF≌△ECD,
∴S△CDE=S△BDF=S△DFC,
∴S△AFC=2$\sqrt{3}$,设AF=a,则CF=$\sqrt{3}$a,
∴$\frac{1}{2}$•a•$\sqrt{3}$a=2$\sqrt{3}$,
∴a=2或-2(舍弃),
∴AF=2,
∵AC=2AF,
∴AC=4,
故答案为4.
∴
点评 本题考查全等三角形的判定和性质、直角三角形的30度角性质,三角形的面积公式的等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考填空题中的压轴题.

练习册系列答案
相关题目
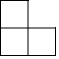 某几何体使用完全相同的正方体搭成的,这个几何体的主视图、俯视图和左视图均是如图所示的图形,则组成该几何体的正方体的个数为( )
某几何体使用完全相同的正方体搭成的,这个几何体的主视图、俯视图和左视图均是如图所示的图形,则组成该几何体的正方体的个数为( )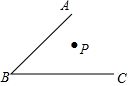 根据下列语句画出图形.
根据下列语句画出图形.