题目内容
4.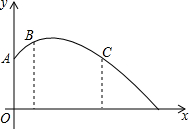 如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=-x2+bx+c表示,且抛物线经过点B($\frac{1}{2}$,$\frac{5}{2}$),C(2,$\frac{7}{4}$).
如图,一个圆形喷水池的中央垂直于水面安装了一个柱形喷水装置OA,O恰好在水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上,按如图所示建立直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式可以用y=-x2+bx+c表示,且抛物线经过点B($\frac{1}{2}$,$\frac{5}{2}$),C(2,$\frac{7}{4}$).请根据以上信息,解答下列问题;
(1)求抛物线的函数关系式,并确定喷水装置OA的高度;
(2)喷出的水流距水面的最大高度是多少米?
(3)若不计其他因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外?
分析 (1)将点B、C坐标代入y=-x2+bx+c列不等式组求出b、c的值即可得解析式,令x=0可得y的值,即喷水装置OA的高度;
(2)将抛物线解析式配方成顶点式即可得其最大值,即水流距水面的最大高度;
(3)令y=0可得对应x的值.
解答 解:(1)根据题意,将点B($\frac{1}{2}$,$\frac{5}{2}$),C(2,$\frac{7}{4}$)代入y=-x2+bx+c,
得:$\left\{\begin{array}{l}{-(\frac{1}{2})^{2}+\frac{1}{2}b+c=\frac{5}{2}}\\{-{2}^{2}+2b+c=\frac{7}{4}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=\frac{7}{4}}\end{array}\right.$,
∴y与x的函数关系式为:y=-x2+2x+$\frac{7}{4}$,
当x=0时,y=$\frac{7}{4}$,
∴喷水装置OA的高度为$\frac{7}{4}$米;
(2)∵y=-x2+2x+$\frac{7}{4}$=-(x-1)2+$\frac{11}{4}$,
∴当x=1时,y取得最大值$\frac{11}{4}$,
故喷出的水流距水面的最大高度是$\frac{11}{4}$米;
(3)当y=0时,解方程-x2+2x+$\frac{7}{4}$=0,
解得:x1=1-$\frac{\sqrt{11}}{2}$,x2=1+$\frac{\sqrt{11}}{2}$,
∵x1=1-$\frac{\sqrt{11}}{2}$<0,不合题意,舍去,
∴x2=1+$\frac{\sqrt{11}}{2}$,
答:水池的半径至少要1+$\frac{\sqrt{11}}{2}$米,才能使喷出的水流不至于落在池外.
点评 本题是二次函数的实际应用,掌握抛物线顶点、与x轴交点、y轴交点的实际意义是解题的关键.

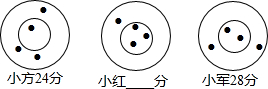 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )| A. | 30分 | B. | 32分 | C. | 33分 | D. | 34分 |
 如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?
如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?
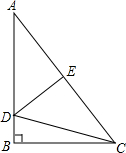 如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$.
如图,Rt△ABC中,∠B=90°,AB=4,BC=3,沿DE折叠使点A与点C刚好重合,则CD的长为$\frac{25}{8}$. 某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )
某班对四月联考数学试卷的10道选择题的答题情况进行统计,每道选择题的分值为3分,制成如图统计图.下列结论:①该班这10道选择题得分的众数为30分;②该班这10道选择题得分的中位数为30分;③该班这10道选择题得分的平均分为28.2分.其中正确结论的个数为( )