题目内容
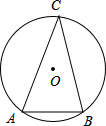已知如图在⊙O中，AB=4cm，∠C=30°，则⊙O的半径是________cm．
4
分析：连接OA，OB，先由圆周角定理求出∠AOB的度数，再判断出△OAB的形状，由此即可得出结论．
解答：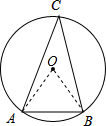
解：连接OA，OB，
∵∠C=30°，
∴∠AOB=2∠C=60°，
∵OA=OB，
∴△OAB是等边三角形，
∴OA=OB=AB=4cm．
故答案为：4．
点评：本题考查的是圆周角定理，根据题意作出辅助线，构造出圆心角是解答此题的关键．
分析：连接OA，OB，先由圆周角定理求出∠AOB的度数，再判断出△OAB的形状，由此即可得出结论．
解答：
解：连接OA，OB，∵∠C=30°，
∴∠AOB=2∠C=60°，
∵OA=OB，
∴△OAB是等边三角形，
∴OA=OB=AB=4cm．
故答案为：4．
点评：本题考查的是圆周角定理，根据题意作出辅助线，构造出圆心角是解答此题的关键．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
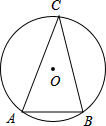已知如图在⊙O中，AB=4cm，∠C=30°，则⊙O的半径是
已知如图在△ABC中，∠ACB=90°，CD⊥AB于D，∠A的平分线交CD于F，BC于E，过点E作EH⊥AB于H．求证：EC=CF=EH．
，sin∠BCE=
. 求CE的长.
AB="CB " (已知)