题目内容
如图，BE、CF是△ABC的角平分线，∠A=40°．则∠BOC=____度．
- A.70
- B.110
- C.120
- D.140
B
分析：由于∠A=40°，根据三角形的内角和定理，得∠ABC与∠ACB的度数和，再由角平分线的定义，得∠OBC+∠OCB的度数，进而求出∠BOC的度数．
解答：∵∠A=40°，
∴∠ABC+∠ACB=180°-40°=140°，
∵BE、CF是△ABC的角平分线，
∴∠OBC+∠OCB=
（∠ABC+∠ACB）=70°，
∴∠BOC=180°-（∠OBC+∠OCB）=180°-70°=110°．
故选B．
点评：本题主要考查了角平分线的定义、三角形的内角和定理等知识．
分析：由于∠A=40°，根据三角形的内角和定理，得∠ABC与∠ACB的度数和，再由角平分线的定义，得∠OBC+∠OCB的度数，进而求出∠BOC的度数．
解答：∵∠A=40°，
∴∠ABC+∠ACB=180°-40°=140°，
∵BE、CF是△ABC的角平分线，
∴∠OBC+∠OCB=
（∠ABC+∠ACB）=70°，∴∠BOC=180°-（∠OBC+∠OCB）=180°-70°=110°．
故选B．
点评：本题主要考查了角平分线的定义、三角形的内角和定理等知识．
练习册系列答案
相关题目
如图，BE、CF是△ABC的角平分线，∠A=50°，则∠BOC的度数是（ ）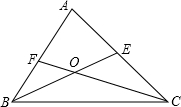
| A、50° | B、65° | C、115° | D、110° |
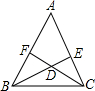如图，BE，CF是△ABC的角平分线，∠A=65°，那么BDC等于（ ）| A、122.5° | B、187.5° | C、178.5° | D、115° |
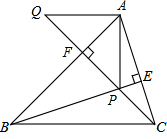如图，BE、CF是△ABC的高，且BP=AC，CQ=AB．求证：AP⊥AQ．
如图，BE、CF是△ABC的角平分线，∠ABC=80°，∠ACB=60°，BE、CF相交于D，则∠CDE的度数是（ ）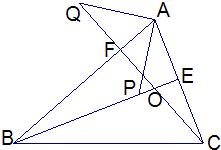
如图，BE、CF是△ABC的高，它们相交于点O，点P在BE上，Q在CF的延长线上且BP=AC，CQ=AB，