题目内容
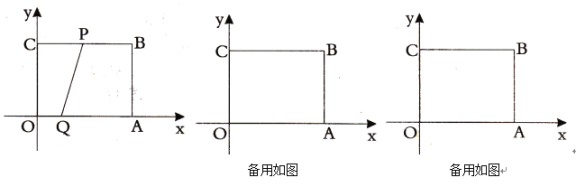
【题目】如图,已知在平面直角坐标系![]() 中,四边形
中,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒
方向以每秒![]() 个单位长度的速度运动;同时动点
个单位长度的速度运动;同时动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴正半轴方向以每秒
轴正半轴方向以每秒![]() 个单位长度的速度运动.设点
个单位长度的速度运动.设点![]() ,点
,点![]() 的运动时间为
的运动时间为![]() .
.
(1)当![]() 时,按要求回答下列问题
时,按要求回答下列问题
①![]() ______________;
______________;
②求经过![]() ,
,![]() ,
,![]() 三点的抛物线
三点的抛物线![]() 的解析式,若将抛物线
的解析式,若将抛物线![]() 在
在![]() 轴上方的部分图象记为
轴上方的部分图象记为![]() ,已知直线
,已知直线![]() 与
与![]() 有两个不同的交点,求
有两个不同的交点,求![]() 的取值范围;
的取值范围;
(2)连接![]() ,点
,点![]() ,
,![]() 在运动过程中,记
在运动过程中,记![]() 与矩形
与矩形![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 与
与![]() 的函数解析式.
的函数解析式.
【答案】(1)①3;②y=-![]() x2+3x; 0≤b<
x2+3x; 0≤b<![]() ;(2)当0≤t≤2时,S=3t;当2<t≤4时,S=24-
;(2)当0≤t≤2时,S=3t;当2<t≤4时,S=24-![]() -3t;当t>4时,S=
-3t;当t>4时,S=![]() .
.
【解析】
(1)①过Q作QM⊥BC,即可在直角三角形中求得tan∠QPC;②设抛物线的解析式,将点O、P、A代入即可求得抛物线方程;将一次函数与抛物线方程联立,由直线与G1有2个交点得到![]() >0,b≥0,求得b的范围.(2)讨论三种情况:当0≤t≤2时,当2<t≤4时,当t>4时,分别求得S与t之间的函数解析式.
>0,b≥0,求得b的范围.(2)讨论三种情况:当0≤t≤2时,当2<t≤4时,当t>4时,分别求得S与t之间的函数解析式.
解:(1)①过Q作QM⊥BC,tan∠QPC=![]() =3;
=3;
②A(4,0)O(0,0)P(2,3)设抛物线的解析式为y=ax2+bx+c,
把A(4,0)O(0,0)P(2,3)代入y=ax2+bx+c得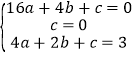 ,
,
解得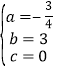 .
.![]() y=
y=![]() x2+3x.
x2+3x.
联立直线 y=![]() x+b与 y=-
x+b与 y=-![]() x2+3x,得
x2+3x,得 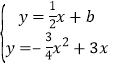 则-
则-![]() x2+3x=
x2+3x=![]() x+b,
x+b,
∵直线![]() x+b 与 G1 有 两 个 不 同 交 点,
x+b 与 G1 有 两 个 不 同 交 点,
∴方程-![]() x2+3x=
x2+3x=![]() x+b有2个不同解,
x+b有2个不同解,
∴![]() >0即
>0即![]() ,
,
b<![]() ,
,
又由直线与G1交于x轴上方,∴b≥0,
∴b的范围为![]() .
.
(2)当0≤t≤2时,S=3t;当2<t≤4时,S=2![]() ;当t>4时,S=
;当t>4时,S=![]() .
.
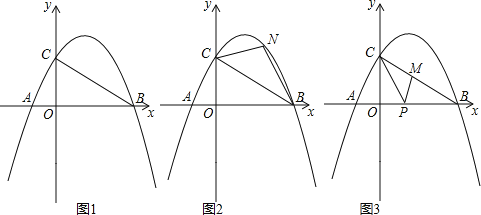
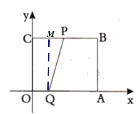
当0≤t≤2时,如图1,由题意可知CP=2t,∴S=S△PCQ=![]() ×2t×3=3t;
×2t×3=3t;
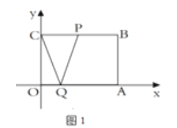
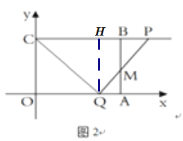
当2<t≤4时,如图2:
过Q作QH⊥CP于H,BP=2t-4,HP=HC=t,HQ=3,
∵BM∥HQ,
∴△PBM∽△PHQ,
∴![]() .
.
即![]() ,
,
∴BM=![]() ,
,
∴AM=3- BM=![]() ,
,
![]()
![]()
![]()
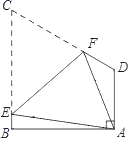
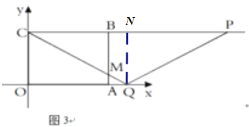
当P在CB延长线上,Q在OA延长线上时,即t>4时,如图3,
CQ与AB交于M点,过Q做![]() ,
,
则![]() ,
,![]()
![]() 即
即![]() ,故有
,故有![]() .
.
面积为: ![]() (t > 4)
(t > 4)

 智慧小复习系列答案
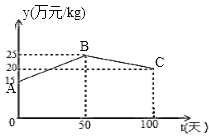
智慧小复习系列答案【题目】经过市场调查得知,某种商品的销售期为100天,设该商品销量单价为y(万元/kg),y与时间t(天)函数关系如下图所示,其中线段AB表示前50天销售单价y(万元/kg)与时间t(天)的函数关系;线段BC的函数关系式为y=-![]() t+m.该商品在销售期内的销量如下表:
t+m.该商品在销售期内的销量如下表:
时间t(天) | 0<t≤50 | 50<t≤100 |
销量(kg) | 200 |
|
(1)分别求出当0<t≤50和50<t≤100时y与t的函数关系式;
(2)设每天的销售收入为w(万元),则当t为何值时,w的值最大?求出最大值;