题目内容
18.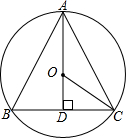 已知正三角形ABC的面积为9$\sqrt{3}$cm,求这个正三角形的边长、边心距、半径、周长.
已知正三角形ABC的面积为9$\sqrt{3}$cm,求这个正三角形的边长、边心距、半径、周长.
分析 由正三角形的性质和三角函数得出AD=AB•sin60°=$\frac{\sqrt{3}}{2}$AB,由正三角形的面积即可得出AB=6cm,得出三角形的周长,由正三角形ABC的面积=三个三角形的面积和,即可得出正三角形的边心距,正三角形的半径=边心距的2倍,即可得出结果.
解答 解:在正三角形ABC中,AD=AB•sin60°=$\frac{\sqrt{3}}{2}$AB,
∵△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{\sqrt{3}}{4}$AB2=9$\sqrt{3}$,
解得:AB=6(cm),
∴AB+BC+AC=3×6=18(cm),
又∵正三角形ABC的面积=3×$\frac{1}{2}$BC•OD=9$\sqrt{3}$,
解得:OD=$\sqrt{3}$,
∴OC=2OD=2$\sqrt{3}$cm,
即这个正三角形的边长为6cm,边心距为$\sqrt{3}$cm,半径为2$\sqrt{3}$cm,周长为18cm.
点评 本题考查了正三角形和圆的关系、正三角形的性质、三角函数、正三角形的边长、边心距、半径、周长的计算方法;熟练掌握正三角形的性质,熟记正三角形的边长、边心距、半径之间的关系是解决问题的关键.

练习册系列答案
相关题目
3.2015年3月30日21时52分,搭载首颗新一代北斗导航卫星的长征三号丙运载火箭在西昌卫星发射中心点火发射,若该运载火箭发射前23秒记作-23秒,则+15秒表示的是( )
| A. | 该运载火箭进入太空15秒 | B. | 该运载火箭停止发射15秒 | ||
| C. | 该运载火箭发射后15秒 | D. | 以上都不正确 |
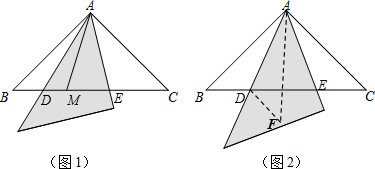
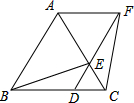 如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF.
如图,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF.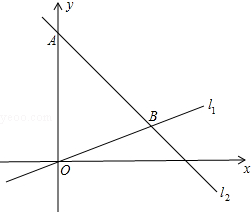 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).