Question

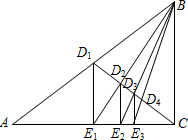在直角三角形ABC中，∠ACB=90°，D₁是斜边AB的中点，过点D₁作D₁E₁⊥AC于点E₁，连接BE₁，交CD₁于点D₂，过点D₂作D₂E₂⊥AC于点E₂，连接BE₂交CD₁于点D₃，过点D₃作D₃E₃⊥AC于点E₃，…如此继续，可以依次得到D₄，D₅，…，D_n，已知△ABC面积为1，分别记△BD₁E₁，△BD₂E₂，△BD₃E₃，…，△BD_nE_n的面积为S₁，S₂，S₃，…，S_n，则S_n=

 

．

Answer 1

考点：相似三角形的判定与性质

专题：规律型

分析：根据直角三角形的性质以及相似三角形的性质解答即可．

解答：解：易知D₁E₁∥BC，∴△BD₁E₁与△CD₁E₁同底同高，面积相等，以此类推；
根据直角三角形的性质以及相似三角形的性质可知：D₁E₁=

1

2

BC，CE₁=

1

2

AC，S₁=

1

22

S_△ABC；
∴在△ACB中，D₂为其重心，
∴D₂E₁=

1

3

BE₁，
∴D₂E₂=

1

3

BC，CE₂=

1

3

AC，S₂=

1

32

S_△ABC，
∵D₂E₂：D₁E₁=2：3，D₁E₁：BC=1：2，
∴BC：D₂E₂=2D₁E₁：

2

3

D₁E₁=3，
∴CD₃：CD₂=D₃E₃：D₂E₂=CE₃：CE₂=3：4，
∴D₃E₃=

3

4

D₂E₂=

3

4

×

1

3

BC=

1

4

BC，CE₃=

3

4

CE₂=

3

4

×

1

3

AC=

1

4

AC，S₃=

1

42

S_△ABC…；
∴S_n=

1

(n+1)2

S_△ABC．
故答案为：

1

(n+1)2

S_△ABC．

点评：考查了相似三角形的判定与性质，解决本题的关键是据直角三角形的性质以及相似三角形的性质得到第一个三角形的面积与原三角形的面积的规律．也考查了重心的性质即三角形三边中线的交点到顶点的距离等于它到对边中点距离的两倍．