题目内容
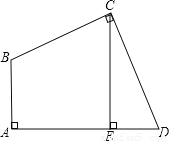
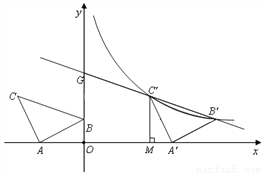
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0, d)、C(-3,2).
(1)求d的值;
(2)将△ABC沿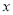 轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
轴的正方向平移a个单位,在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上.请求出这个反比例函数和此时直线B′C′的解析式;
(3)在(2)的条件下,直线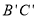 交y轴于点G,作
交y轴于点G,作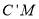 ⊥
⊥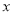 轴于
轴于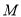 .
. 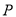 是线段
是线段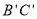 上的一点,若△
上的一点,若△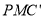 和△
和△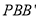 面积相等,求点
面积相等,求点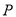 坐标.
坐标.
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
二次函数y=ax2+bx+c的部分对应值如下表.利用二次函数的图象可知,当函数值y<0时,x的取值范围是
( )
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
A. x<0或x>2 B. 0<x<2 C. x<﹣1或x>3 D. ﹣1<x<3
D 【解析】从表格可以看出,当x=﹣1或3时,y=0; 因此当﹣1<x<3时,y<0. 故选D.

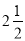 ,﹣1.5;
,﹣1.5;

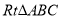 中,
中, 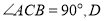 为斜边
为斜边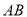 的中点,
的中点, 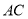 =6 cm,
=6 cm, 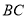 =8 cm,则
=8 cm,则 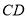 的长为___________cm.
的长为___________cm.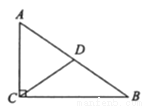
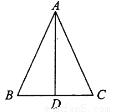
 B.
B.  C.
C. 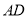 平分
平分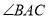 D.
D. 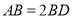
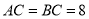 m,
m, 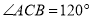 ,
, 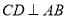 于点
于点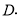 求
求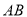 的长度.
的长度.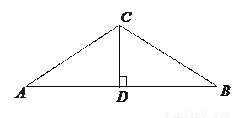
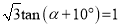 ,则锐角 α=________
,则锐角 α=________