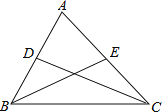
题目内容
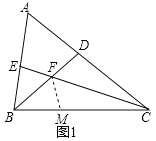
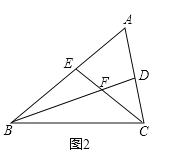
【题目】如图，已知
中，延长
边上的中线
到
，使
，延长
边上的中线
到
，使
，连接
．
（1）补全图形；
（2）的大小关系如何？证明你的结论；
（3）
三点的位置关系如何？证明你的结论．
【答案】（1）答案见解析；（2）
，证明见解析；（3）
三点共线，证明见解析．
【解析】
（1）按照题目中的要求补全图形即可；
（2）根据已知条件利用
可以证得
、
，再由全等三角形的性质得到
、
，最后等量代换即可得证；
（3）根据全等三角形的性质、三角形内角和定理以及平角的定义即可得证
、
、
三点共线．
解：（1）补全图形，如图所示；
（2），理由为：
在
和
中，
∴
∴
在
和
中，
∴
∴
∴
（3）、、三点共线，理由为：
∵，
∴
，
∵
∴
∴、、三点共线．
故答案是：（1）答案见解析；（2），证明见解析；（3）、、三点共线，证明见解析．
练习册系列答案
相关题目
【题目】在不透明的袋子中有四张标有数字1，2，3，4的卡片，小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下：
小华列出表格如下：
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | （1，1） | （2，1） | （3，1） | （4，1） |
2 | （1，2） | （2，2） | ① | （4，2） |
3 | （1，3） | （2，3） | （3，3） | （4，3） |
4 | （1，4） | （2，4） | （3，4） | （4，4） |
回答下列问题：
（1）根据小明画出的树形图分析，他的游戏规则是：随机抽出一张卡片后 （填“放回”或“不放回”），再随机抽出一张卡片；
（2）根据小华的游戏规则，表格中①表示的有序数对为 ；
（3）规定两次抽到的数字之和为奇数的获胜，你认为淮获胜的可能性大？为什么？
