题目内容
【题目】如图1,已知ED垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.
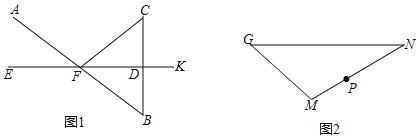
(1)求证:∠AFE=∠CFD;
(2)如图2.在△GMN中,P为MN上的任意一点.在GN边上求作点Q,使得∠GQM=∠PQN,保留作图痕迹,写出作法并作简要证明.
【答案】(1)证明见解析;(2)答案见解析.
【解析】
(1)根据垂直平分线的性质证明三角形CFB是等腰三角形,进而证明∠AFE=∠CFD;
(2)作点P关于GN的对称点P′,连接P′M交GN于点Q,结合(1)即可证明∠GQM=∠PQN.
(1)∵ED垂直平分BC,
∴FC=FB,
∴△FCB是等腰三角形.
∵FD⊥BC,
由等腰三角形三线合一可知:
FD是∠CFB的角平分线,
∴∠CFD=∠BFD.
∵∠AFE=∠BFD,
∴∠AFE=∠CFD.
(2)作点P关于GN的对称点P',
连接P'M交GN于点Q,
点Q即为所求.

∵QP=QP',
∴△QPP'是等腰三角形.
∵QN⊥PP',
∴QN是∠PQP'的角平分线,
∴∠PQN=∠P'QN.
∵∠GQM=∠P'QN,
∴∠GQM=∠PQN.

练习册系列答案
相关题目
【题目】近年来网约车十分流行,初三某班学生对“美团”和“滴滴”两家网约车公司各10名司机月收入进行了一项抽样调查,司机月收入(单位:千元)如图所示:

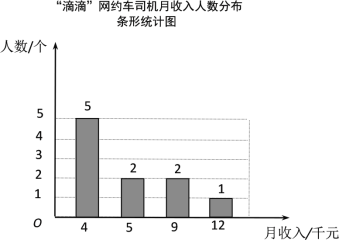
根据以上信息,整理分析数据如下:
平均月收入/千元 | 中位数/千元 | 众数/千元 | 方差/千元2 | |
“美团” | ① | 6 | 6 | 1.2 |
“滴滴” | 6 | ② | 4 | ③ |
(1)完成表格填空;
(2)若从两家公司中选择一家做网约车司机,你会选哪家公司,并说明理由.