题目内容
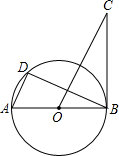
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC.
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=
,求AD的长.(结果保留根号)
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=
| 5 |

(1)证明:∵AD∥OC,
∴∠A=∠COB,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠D=90°,∠CBO=90°,
即∠A=∠COB,∠D=∠CBO,
∴△ADB∽△OBC.
(2)OB=
AB=1,
在△OBC中,由勾股定理得:OC=
=
,
∵△ADB∽△OBC,
∴
=
,
∴
=
解得:AD=
.
答:AD的长是
.
∴∠A=∠COB,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠D=90°,∠CBO=90°,
即∠A=∠COB,∠D=∠CBO,
∴△ADB∽△OBC.
(2)OB=
| 1 |
| 2 |
在△OBC中,由勾股定理得:OC=
| OB2+BC2 |
| 6 |
∵△ADB∽△OBC,
∴
| AD |
| OB |
| AB |
| OC |
∴
| AD |
| 1 |
| 2 | ||
|
解得:AD=
| ||
| 3 |
答:AD的长是
| ||
| 3 |

练习册系列答案
相关题目








