题目内容
【题目】如图，抛物线y=ax2﹣4ax+3a（a＞0），与y轴交于点A，在x轴的正半轴上取一点B，使OB=2OA，抛物线的对称轴与抛物线交于点C，与x轴交于点D，与直线AB交于点E，连接BC．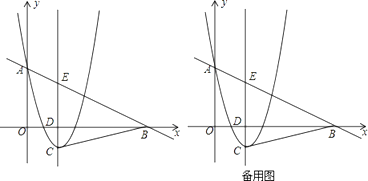
（1）求点B，C的坐标（用含a的代数式表示）；
（2）若△BCD与△BDE相似，求a的值；
（3）连接OE，记△OBE的外心为M，点M到直线AB的距离记为h，请探究h的值是否会随着a的变化而变化？如果变化，请写出h的取值范围；如果不变，请求出h的值．
【答案】
（1）
解：由抛物线的解析式可知：点C的坐标为（2，﹣a），
令x=0代入y=ax2﹣4ax+3a，
∴y=3a，
∴OA=3a，
∵OB=2OA=6a，
∴点B的坐标为（6a，0）
（2）
解：由（1）可知：OD=2，CD=a，OB=6a，
若点B在点D的右侧时，如图1，
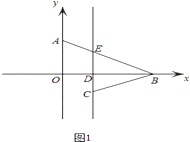
则6a＞2，
∴a＞ 
，
∴BD=6a﹣2，
当∠DBC=∠EBD时，
∴tan∠DBC=tan∠EBD= 
= 
，
∴ 
，
∴ 
= ，
∴a= ，
当∠DCB=∠EBD时，
∴tan∠DCB=tan∠EBD= ，
∴ 
，
∴ 
，
∴a= 
，
若点B在点D的左侧时，如图2，
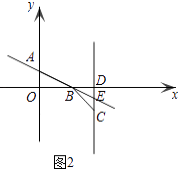
则0＜6a＜2，
∴0＜a＜ ，
∴BD=2﹣6a，
当∠DBC=∠EBD时，
∴tan∠DBC=tan∠EBD= = ，
∴ ，
∴ 
= ，
∴a= 
，
当∠DCB=∠EBD时，
∴tan∠DCB=tan∠EBD= ，
∴ ，
∴ 
= ，
∴a= 
，
若点B与点D重合时，
则6a=2，
∴a= ，
此情况不存在△BCD与△BDE，
综上所述，a的值为 、 、 和
（3）
解：由题意知：点M在OB和BE的垂直平分线上，
设OB和BE的垂直平分线交于点M，
其中OB的垂直平分线与OB交于点G，
BE的垂直平分线交OB于点H，交BE于点F
当点B在点D的右侧时，如图3，
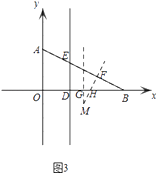
∴6a＞2，
∴a＞ ，
∴BD=6a﹣2，
∵tan∠EBD= ，
∴ED= BD=3a﹣1，
由勾股定理可求得：BE=3 
a﹣ ，
∴BF= BE= 
，
∴HF= BF= 
，
∴由勾股定理可求得：BH= 
，
∴HG=BG﹣BH= 
，
∵∠GMH=∠EBD，
∴sin∠GMH=sin∠EBD= 
，
∴MH= HG= 
，
∴MF=MH+HF= ，
当点B在点D的左侧时，如图：
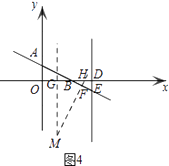
∴0＜a＜ ，
∴BD=OD﹣OB=2﹣6a，
∵tan∠ABO=tan∠DBE= ，
∴DE= BD=1﹣3a，
∴由勾股定理可求得：BE= ﹣3 a，
∴BF= BE= 
，
∴HF= BF= 
，
由勾股定理求得：BH= 
，
∵GB= OB=3a，
∴GH=GB+BH= ，
∵∠HBF+∠BHF=90°，
∠GMH+∠BHF=90°，
∴∠HBF=∠GMH，
∴sin∠HBF=sin∠GMH= ，
∴MH= GH= ，
∴MF=MH﹣HF= ，
当点B与点D重合时，
此时a= ，
此情况不符合题意，舍去
综上所述，点M到直线AB的距离不会变化，始终为 ．
【解析】（1）令x=0代入抛物线可得y=3a，即OA=3a，因为OB=2OA，所以B的坐标为（6a，0），点C时抛物线的顶点，利用顶点坐标公式即可求出C的坐标为（2，﹣a）；（2）由于点B的位置不确定，所以分三种情况讨论，一是点B在点D的左侧，二是点B在点D的右侧，三是点B与点D重合，其中第三种情况是不存在△BCD与△BDE；另外，△BCD与△BDE相似时，有两种情况，一是∠DBC=∠EBD，二是∠DBE=∠DBC，利用相似三角形的性质即可求出a的值；（3）由于点B的位置不确定，所以分三种情况讨论，一是点B在点D的左侧，二是点B在点D的右侧，三是点B与点D重合，其中第三种情况是不存在△OBE，由题意知：点M在OB和BE的垂直平分线上，设OB和BE的垂直平分线交于点M，其中OB的垂直平分线与OB交于点G，BE的垂直平分线交OB于点H，交BE于点F，利用相似三角形的性质求出MF的长度即可；
