题目内容
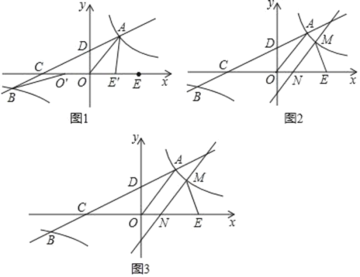
【题目】如图1,在平面直角坐标系xOy中,双曲线![]() 与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
与直线y=ax+b(a≠0)交于A、B两点,直线AB分别交x轴、y轴于C、D两点,E为x轴上一点.已知OA=OC=OE,A点坐标为(3,4).
(1)将线段OE沿x轴平移得线段O′E′(如图1),在移动过程中,是否存在某个位置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点O′的坐标;若不存在,请说明理由;
(2)将直线OA沿射线OE平移,平移过程中交![]() 的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
的图象于点M(M不与A重合),交x轴于点N(如图3).在平移过程中,是否存在某个位置使△MNE为以MN为腰的等腰三角形?若存在,求出M的坐标;若不存在,请说明理由.
【答案】(1)存在,|BO′﹣AE′|的最大值为![]() ,此时点O′的坐标(﹣
,此时点O′的坐标(﹣![]() ,0);(2)存在,M(
,0);(2)存在,M(![]() )或(8,
)或(8,![]() ).
).
【解析】
(1)把A向左平移5个单位得A1(-2,4),作B关于x轴的对称点B1,则有|BO′-AE′|=|BO′-A1O′|=B1O′-A1O′|≤A1B1,想办法求出A1B1,直线A1B1的解析式即可解决问题;
(2)设M(m,![]() ),则N(m
),则N(m![]() ,0),NE2=(5-m+
,0),NE2=(5-m+![]() )2,ME2=(5-m)2+(
)2,ME2=(5-m)2+(![]() )2,MN2=(
)2,MN2=(![]() )2+(
)2+(![]() )2,分MN=EM,MN=NE两种情形,分别构建方程即可解决问题.
)2,分MN=EM,MN=NE两种情形,分别构建方程即可解决问题.
(1)如图1中,
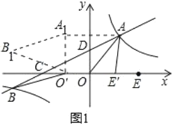
∵A(3,4),
∴OA=![]() =5,
=5,
∵OA=OC=OE,
∴OA=OC=OE=5,
∴C(﹣5,0),E(5,0),
把A、C两点坐标代入y=ax+b得到![]() ,
,
解得![]() ,
,
∴直线的解析式为:![]() ,
,
把A(3,4)代入y=![]() 中,得到k=12,
中,得到k=12,
∴反比例函数的解析式为y=![]() ,
,
把A向左平移5个单位得A1(﹣2,4),作B关于x轴的对称点B1,
则有|BO′﹣AE′|=|BO′﹣A1O′|=|B1O′﹣A1O′|≤A1B1,
直线AC:![]() ,
,
双曲线:![]() ,
,
∴B(﹣8,﹣![]() ),B1(﹣8,
),B1(﹣8,![]() ),
),
∴A1B1=![]() ,
,
直线A1B1:![]() ,
,
令y=0,可得x=﹣![]() ,
,
∴O′(﹣![]() ,0).
,0).
∴|BO′﹣AE′|的最大值为![]() ,此时点O′的坐标(﹣
,此时点O′的坐标(﹣![]() ,0).
,0).
(2)设M(m,![]() ),则N(m﹣
),则N(m﹣![]() ,0),
,0),
∴NE2=(5﹣m+![]() )2,ME2=(5﹣m)2+(
)2,ME2=(5﹣m)2+(![]() )2,MN2=(
)2,MN2=(![]() )2+(
)2+(![]() )2
)2
若MN=ME,则有,(5﹣m)2+(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得:m=![]() 或
或![]() (舍弃),
(舍弃),
∴M(![]() ,
,![]() ),
),
若MN=NE,则有(5﹣m+![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,解得m=8或3(舍弃),
)2,解得m=8或3(舍弃),
∴M(8,![]() ),
),
综上所述,满足条件的点M的坐标为(![]() ,
,![]() )或(8,
)或(8,![]() ).
).

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】在初中阶段的函数学习中,我们经历了“确定函数的解析式利用函数图象研究其性质﹣运用函数解决问题”的学习过程.在画函数图象时,我们可以通过描点或平移或翻折等方法画出函数图象、下面我们対函数y=|![]() ﹣1|展开探索,请补充以下探索过程:
﹣1|展开探索,请补充以下探索过程:
(1)列表
x | … | ﹣1 | ﹣ | ﹣ | ﹣ | 0 |
|
|
| … |
|
|
| 2 |
|
|
| 3 | … | |
y | … |
|
|
|
| 2 |
| 3 | a | … | 3 | 1 |
| 0 |
|
| b |
| … | |
直接写出函数自变量x的取值范围,及a= ,b= ;
(2)在给出的平面直角坐标系中,请用你喜欢的方法画出这个函数的图象,并写出这个函数的一条性质: .
(3)若方程|![]() ﹣1|=m有且只有一个解,直接写出m的值: .
﹣1|=m有且只有一个解,直接写出m的值: .