题目内容
10. 如图,矩形ABCD的边AD是菱形AEDF的一条对角线,且点E在矩形ABCD的边BC上.
如图,矩形ABCD的边AD是菱形AEDF的一条对角线,且点E在矩形ABCD的边BC上.(1)求证:△ABE≌△DCE;
(2)直接写出当矩形边长AD与AB之间满足什么关系时,菱形AEDF为正方形.
分析 (1)由矩形的性质得出AB=DC,∠B=∠C=90°,由菱形的性质得出AE=DE,由HL证明Rt△ABE≌Rt△DCE即可;
(2)由全等三角形的性质得出BE=CE,∠AEB=∠DEC,由AD=2AB,证出△ABE是等腰直角三角形,得出∠AEB=45°,证出∠AED=90°,即可得出菱形AEDF为正方形.
解答 (1)证明:∵四边形ABCD是矩形,
∴AB=DC,∠B=∠C=90°,AD=BC,
∵四边形AEDF是菱形,
∴AE=DE,
在Rt△ABE和Rt△DCE中,$\left\{\begin{array}{l}{AE=DE}\\{AB=DC}\end{array}\right.$,
∴Rt△ABE≌Rt△DCE(HL);
(2)解:当AD=2AB时,菱形AEDF为正方形;理由如下:
∵Rt△ABE≌Rt△DCE,
∴BE=CE,∠AEB=∠DEC,
∵AD=2AB,AD=BC,
∴AB=BE,
∴△ABE是等腰直角三角形,
∴∠AEB=45°,
∴∠DEC=45°,
∴∠AED=180°-45°-45°=90°,
∴菱形AEDF为正方形.
点评 本题考查了矩形的性质、全等三角形的判定与性质、菱形的性质、正方形的判定、等腰直角三角形的判定与性质;熟练掌握矩形和菱形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
20. 如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,分别以AC、BC为直径画半圆,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,分别以AC、BC为直径画半圆,则图中阴影部分的面积为( )
 如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,分别以AC、BC为直径画半圆,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,分别以AC、BC为直径画半圆,则图中阴影部分的面积为( )| A. | 10π-8 | B. | 10π-16 | C. | 10π | D. | 5π |
20.已知∠1=40°,则∠1的余角的度数是( )
| A. | 40° | B. | 50° | C. | 140° | D. | 150° |
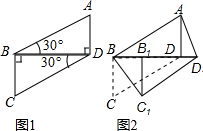
 如图,△ABC是等边三角形,D,E两点分别在AB,BC的延长线上,BD=CE,连接AE,CD.求证:∠E=∠D.
如图,△ABC是等边三角形,D,E两点分别在AB,BC的延长线上,BD=CE,连接AE,CD.求证:∠E=∠D.