题目内容
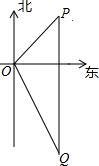 小明在某风景区的观景台O处观测到东北方向的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东30°,且与O相距6km的Q处.如图.货船的航行速度是
小明在某风景区的观景台O处观测到东北方向的P处有一艘货船,该船正向南匀速航行,30分钟后再观察时,该船已航行到O的南偏东30°,且与O相距6km的Q处.如图.货船的航行速度是考点:解直角三角形的应用-方向角问题
专题:
分析:先解直角△OAQ,得出OA=
OQ=3km,AQ=
OA=3
km,再解直角△OAP,得出PA=OA=3km,则PQ=PA+AQ=(3+3
)km,然后根据速度=路程÷时间即可求出货船的航行速度.
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
解答: 解:如图,在直角△OAQ中,∠OAQ=90°,∠Q=30°,OQ=6km,
解:如图,在直角△OAQ中,∠OAQ=90°,∠Q=30°,OQ=6km,
∴OA=
OQ=3km,AQ=
OA=3
km.
在直角△OAP中,∠OAP=90°,∠AOP=45°,OA=3km,
∴PA=OA=3km,
∴PQ=PA+AQ=(3+3
)km,
∴货船的航行速度是(3+3
)÷
=6+6
(km/h).
故答案为(6+6
).
 解:如图,在直角△OAQ中,∠OAQ=90°,∠Q=30°,OQ=6km,
解:如图,在直角△OAQ中,∠OAQ=90°,∠Q=30°,OQ=6km,∴OA=
| 1 |
| 2 |
| 3 |
| 3 |
在直角△OAP中,∠OAP=90°,∠AOP=45°,OA=3km,
∴PA=OA=3km,
∴PQ=PA+AQ=(3+3
| 3 |
∴货船的航行速度是(3+3
| 3 |
| 1 |
| 2 |
| 3 |
故答案为(6+6
| 3 |
点评:本题主要考查了解直角三角形的应用-方向角问题,求出AQ与AP的长度是解题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
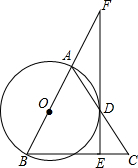 如图,在△ABC中,AB=BC,以AB为直径的⊙0与AC于点D,作DE⊥BC垂足为E,延长ED交BA的延长线于点F.
如图,在△ABC中,AB=BC,以AB为直径的⊙0与AC于点D,作DE⊥BC垂足为E,延长ED交BA的延长线于点F. 函数y=kx+b的大致图象如图所示,则当x<0时,y的取值范围是
函数y=kx+b的大致图象如图所示,则当x<0时,y的取值范围是 如图,在平面直角坐标系中,点P的坐标为(4,2),点A的坐标为(1,0),以点P为圆心,AP长为半径作弧,与x轴交于点B,则点B的坐标为
如图,在平面直角坐标系中,点P的坐标为(4,2),点A的坐标为(1,0),以点P为圆心,AP长为半径作弧,与x轴交于点B,则点B的坐标为