题目内容
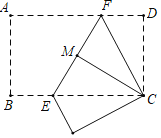
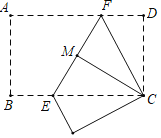
【题目】如图，把一张矩形纸片折叠，点A与点C重合，折痕为EF，再将△CDF沿CF折叠，点D恰好落在EF上的点M处，若BC＝6厘米，则EF的长为_____厘米．
【答案】4
【解析】
由矩形的性质可得AD＝BC＝6cm，∠D＝90°，AD∥BC，由折叠的性质可得CD＝CM，∠D＝∠FMC＝60°，FD＝FM，∠DFC＝∠MFC，AF＝CF，∠AFE＝∠EFC，由平角的定义可得AFE＝∠EFC＝∠DFC＝60°，可证△EFC是等边三角形，可求解.
解：∵四边形ABCD是矩形
∴AD＝BC＝6cm，∠D＝90°，AD∥BC
∵把一张矩形纸片折叠，点A与点C重合，
∴AF＝CF，∠AFE＝∠EFC
∵将△CDF沿CF折叠，点D恰好落在EF上的点M处，
∴CD＝CM，∠D＝∠FMC＝60°，FD＝FM，∠DFC＝∠MFC
∴∠AFE＝∠EFC＝∠DFC，且∠AFE+∠EFC+∠DFC＝180°
∴∠AFE＝∠EFC＝∠DFC＝60°，
∴∠FCD＝30°
∴FC＝2FD，
∴AF＝2FD，
∵AD= BC＝6厘米，
∴FD＝2厘米，AF＝4厘米＝FC，
∵AD//BC
∴∠AFE＝∠FEC＝60°，且∠EFC＝60°
∴△EFC是等边三角形
∴EF＝FC＝4厘米
故答案为：4
【题目】小明根据学习函数的经验，对函数y＝
+1的图象与性质进行了探究．下面是小明的探究过程，请补充完整：
（1）函数y＝+1的自变量x的取值范围是 ；
（2）下表列出了y与x的几组对应值，请写出m，n的值：m＝ ，n＝ ；
x | … | ﹣ | ﹣1 | ﹣ | 0 |
|
| 2 |
| 3 |
| … |
y | … |
| m |
| 0 | ﹣1 | n | 2 |
|
|
| … |
（3）在如图所示的平面直角坐标系中，描全上表中以各对对应值为坐标的点，并画出该函数的图象．
（4）结合函数的图象，解决问题：
①写出该函数的一条性质：
②当函数值+1＞
时，x的取值范围是：
③方程+1＝x的解为：
