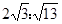题目内容
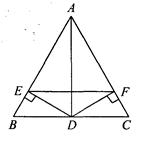
如图,已知△ABC中,BD、CE是高,F是BC中点,连接DE、EF和DF.
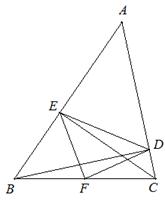
(1)求证:△DEF是等腰三角形;
(2)若∠A=45°,试判断△DEF的形状,并说明理由;
(3)若∠A:∠DFE=5:2,BC=4,求△DEF的面积.

(1)求证:△DEF是等腰三角形;
(2)若∠A=45°,试判断△DEF的形状,并说明理由;
(3)若∠A:∠DFE=5:2,BC=4,求△DEF的面积.
(1)证明见试题解析;(2)△DEF是等腰直角三角形,理由见试题解析;(3)1.
试题分析:(1)由直角三角形斜边上直线的性质可得:EF=
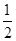 BC=DF;故△DEF为等腰三角形;
BC=DF;故△DEF为等腰三角形;(2)由△BEF和△DFC为等腰三角形和∠A=45°,求出∠EFD的度数即可;
(3)设∠A=5
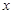 ,则∠DFE=2
,则∠DFE=2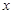 ,用(2)类似的方法求出∠DFE=30°,作出△EDF边DF上的高EG,求出EG的长即可.
,用(2)类似的方法求出∠DFE=30°,作出△EDF边DF上的高EG,求出EG的长即可.试题解析:(1)证明:∵BD、CE是高,F是BC中点,∴EF=
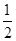 BC=DF,∴△DEF是等腰三角形.
BC=DF,∴△DEF是等腰三角形.(2)△DEF是等腰直角三角形;理由:∵∠A=45°,∴∠EBF+∠DCF=180°-45°=135°,∵EF=
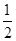 BC=DF,∴∠EBF=∠FEB,同理,∠DCF=∠FDC,∴∠FEB+∠FDC=135°,
BC=DF,∴∠EBF=∠FEB,同理,∠DCF=∠FDC,∴∠FEB+∠FDC=135°,∴∠BFE+∠CFD=180°+180°-135°-135°=90°,∴∠DFE=180°-90°=90°,∴△DEF是等腰直角三角形.
(3)作EG⊥DF于G,设∠A=5
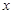 ,∠DFE=2
,∠DFE=2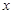 ,∵EF=BF,DF=FC,∴∠FBE=∠BEF,∠FCD=∠FDC,
,∵EF=BF,DF=FC,∴∠FBE=∠BEF,∠FCD=∠FDC,∴∠BFE+∠CFD=180°-2∠FBE+180°-2∠FCD=2(180°-∠FBE-∠FCD)=2∠A=
 ,∵
,∵
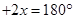 ,∴∠DFE=2
,∴∠DFE=2 ,∵BC=4,∴DF=EF=2,∴EG=1,∴△DEF面积1.
,∵BC=4,∴DF=EF=2,∴EG=1,∴△DEF面积1.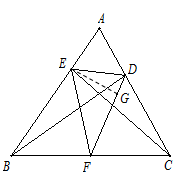

练习册系列答案
相关题目