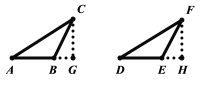��Ŀ����
����Ŀ����������������꼶�ϲ�α���������һ�仰�����ߺ�����һ�ߵĶԽǷֱ���ȵ����������β�һ��ȫ�ȡ�����������һ��̽��ʲô�����ȫ�ȣ�
������˼�������Dz�������������ת���ɷ������ԣ���![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
������̽����
��1����![]() ��
��![]() �����ʱ��
�����ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ���ȫ�ȣ���֤��������ȫ�ȣ���ٳ�������
�Ƿ�ȫ�ȣ���ȫ�ȣ���֤��������ȫ�ȣ���ٳ�������
��2����![]() ��
��![]() ��ֱ��ʱ��
��ֱ��ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ���ȫ�ȣ�ֱ��˵�����ɣ�����Ҫ֤��������ȫ�ȣ���ٳ�������
�Ƿ�ȫ�ȣ���ȫ�ȣ�ֱ��˵�����ɣ�����Ҫ֤��������ȫ�ȣ���ٳ�������
��3����![]() ��
��![]() �Ƕ۽�ʱ��
�Ƕ۽�ʱ��![]() ��
��![]() �Ƿ�ȫ�ȣ���ȫ�ȣ��������ͼ֤��������ȫ�ȣ���ٳ�������
�Ƿ�ȫ�ȣ���ȫ�ȣ��������ͼ֤��������ȫ�ȣ���ٳ�������
���𰸡���1��![]() ��
��![]() ��ȫ�ȣ���������������2��
��ȫ�ȣ���������������2��![]() ��
��![]() ȫ�ȣ����ɼ���������3��
ȫ�ȣ����ɼ���������3��![]() ��
��![]() ȫ�ȣ�֤��������
ȫ�ȣ�֤��������
��������
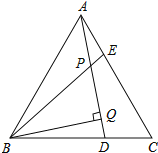
��1��������һ����������κ�һ���۽�����������![]() ���ɣ�
���ɣ�
��2����������ֱ��������ȫ�ȵ��ж�������![]() �������ɵã�
�������ɵã�
��3����ͼ�������������ȸ���������ȫ�ȵ��ж����������ʵó�![]() ���ٸ���ֱ��������ȫ�ȵ��ж����������ʵó�
���ٸ���ֱ��������ȫ�ȵ��ж����������ʵó�![]() ��Ȼ�����������ȫ�ȵ��ж��������ɵ�֤��
��Ȼ�����������ȫ�ȵ��ж��������ɵ�֤��
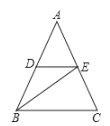
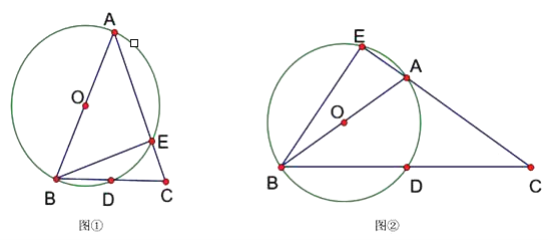
��1��![]() ��
��![]() ��ȫ��
��ȫ��
��������ͼ��ʾ��![]() ������Ȼ
������Ȼ![]() ��
��![]() ��ȫ�ȣ�
��ȫ�ȣ�
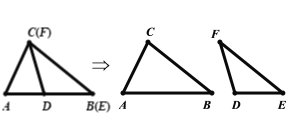
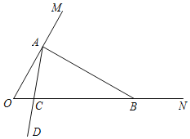
��2��![]() ��
��![]() ȫ��
ȫ��
���ɣ�б�ߺ�һ��ֱ�DZ߷ֱ���ȵ�����ֱ��������ȫ�ȣ���![]() ������
������
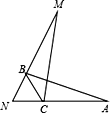
��3��![]() ��
��![]() ȫ�ȣ�֤�����£�
ȫ�ȣ�֤�����£�
��ͼ������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]()
��![]() ����
����![]() ��
��![]() ���Ƕ۽�
���Ƕ۽�
��![]() ����
����![]()
��![]() ��
��![]() ��
�У�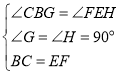
��![]()
��![]()
��![]() ��
��![]() ��
�У�![]()
��![]()
��![]()
��![]() ��
��![]() ��
�У�
��![]() ��
��