题目内容
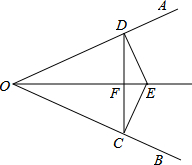 如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F.
如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,连接CD,与∠AOB的平分线交于点F.(1)求证:OE是CD的垂直平分线;
(2)若∠AOB=60°,求OF:FE的值.
分析:(1)根据垂直平分线的性质定理证明.
(2)通过解特殊角三角函数计算.
(2)通过解特殊角三角函数计算.
解答:解:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D是垂足,
∴DE=CE.
在Rt△EDO与Rt△ECO中,
DE=CE,OE为公共边,∠DOE=∠COF,
∴OD=OC.
∵OF为角平分线,
∴OE是CD的垂直平分线.
(2)设OD=a,∠AOB=60°,
∴∠DOE=30°,∠ODF=60°,DF=
OD=
.
OF=
.
∵∠ODE=90°,∠ODF=60°,
∴∠EDF=30°.
在Rt△DEF中,
tan30°=
=
=
,EF=
.
∴OF:FE=
:
=3:1.
∴DE=CE.
在Rt△EDO与Rt△ECO中,
DE=CE,OE为公共边,∠DOE=∠COF,
∴OD=OC.
∵OF为角平分线,
∴OE是CD的垂直平分线.
(2)设OD=a,∠AOB=60°,
∴∠DOE=30°,∠ODF=60°,DF=
| 1 |
| 2 |
| a |
| 2 |
OF=
| ||
| 2 |
∵∠ODE=90°,∠ODF=60°,
∴∠EDF=30°.
在Rt△DEF中,
tan30°=
| EF |
| DF |
| EF | ||
|
| ||
| 3 |
| ||
| 6 |
∴OF:FE=
| ||
| 2 |
| ||
| 6 |
点评:考查了特殊角的三角函数值和角平分线的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
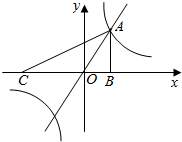 如图,已知点A是一次函数y=2x的图象与反比例函数y=-
如图,已知点A是一次函数y=2x的图象与反比例函数y=-| k |
| x |
| A、(-5,0) |
| B、(-6,0) |
| C、(-5.5,0) |
| D、(-4,0) |
 21、如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G.,求证:AF=GB.
21、如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交边AB于F,∠ADC的平分线DG交边AB于G.,求证:AF=GB. 32、如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点
32、如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.写出你作图的主要步骤并标明你所确定的点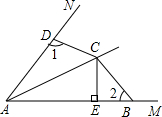 如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=
如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE= 如图,已知点P是反比例函数y=
如图,已知点P是反比例函数y=